A Taylor Series Approach to Correction of Input Errors in Gaussian Process Regression

Gaussian Processes (GPs) are widely recognized as powerful non-parametric models for regression and classification. Traditional GP frameworks predominantly operate under the assumption that the inputs are either accurately known or subject to zero-mean noise. However, several real-world applications such as mobile sensors have imperfect localization, leading to inputs with biased errors. These biases can typically be estimated through measurements collected over time using, for example, Kalman filters. To avoid recomputation of the entire GP model when better estimates of the inputs used in the training data become available, we introduce a technique for updating a trained GP model to incorporate updated estimates of the inputs. By leveraging the differentiability of the mean and covariance functions derived from the squared exponential kernel, a second-order correction algorithm is developed to update the trained GP models. Precomputed Jacobians and Hessians of kernels enable real-time refinement of the mean and covariance predictions. The efficacy of the developed approach is demonstrated using two simulation studies, with error analyses revealing improvements in both predictive accuracy and uncertainty quantification.

Improved Dwell-times for Switched Nonlinear Systems using Memory Regression Extension

This paper presents a switched systems approach for extending the dwell-time of an autonomous agent during GPS-denied operation by leveraging memory regressor extension (MRE) techniques. To maintain accurate trajectory tracking despite unknown dynamics and environmental disturbances, the agent periodically acquires access to GPS, allowing it to correct accumulated state estimation errors. The motivation for this work arises from the limitations of existing switched system approaches, where increasing estimation errors during GPS-denied intervals and overly conservative dwell-time conditions restrict the operational efficiency of the agent. By leveraging MRE techniques during GPS-available intervals, the developed method refines the estimates of unknown system parameters, thereby enabling longer and more reliable operation in GPS-denied environments. A Lyapunov-based switched-system stability analysis establishes that improved parameter estimates obtained through concurrent learning allow extended operation in GPS-denied intervals without compromising closed-loop system stability. Simulation results validate the theoretical findings, demonstrating dwell-time extensions and enhanced trajectory tracking performance.

Fault Detection via Occupation Kernel Principal Component Analysis

The reliable operation of automatic systems is heavily dependent on the ability to detect faults in the underlying dynamical system. While traditional model-based methods have been widely used for fault detection, data-driven approaches have garnered increasing attention due to their ease of deployment and minimal need for expert knowledge. In this paper, we present a novel principal component analysis (PCA) method that uses occupation kernels. Occupation kernels result in feature maps that are tailored to the measured data, have inherent noise-robustness due to the use of integration, and can utilize irregularly sampled system trajectories of variable lengths for PCA. The occupation kernel PCA method is used to develop a reconstruction error approach to fault detection and its efficacy is validated using numerical simulations.

Nonuniqueness and Convergence to Equivalent Solutions in Observer-based Inverse Reinforcement Learning

A key challenge in solving the deterministic inverse reinforcement learning problem online and in real time is the existence of non-unique solutions. Nonuniqueness necessitates the study of the notion of equivalent solutions and convergence to such solutions. While \emph{offline} algorithms that result in convergence to equivalent solutions have been developed in the literature, online, real-time techniques that address nonuniqueness are not available. In this paper, a regularized history stack observer is developed to generate solutions that are approximately equivalent. Novel data-richness conditions are developed to facilitate the analysis and simulation results are provided to demonstrate the effectiveness of the developed technique.

Singular Dynamic Mode Decompositions

This manuscript is aimed at addressing several long standing limitations of dynamic mode decompositions in the application of Koopman analysis. Principle among these limitations are the convergence of associated Dynamic Mode Decomposition algorithms and the existence of Koopman modes. To address these limitations, two major modifications are made, where Koopman operators are removed from the analysis in light of Liouville operators (known as Koopman generators in special cases), and these operators are shown to be compact for certain pairs of Hilbert spaces selected separately as the domain and range of the operator. While eigenfunctions are discarded in the general analysis, a viable reconstruction algorithm is still demonstrated, and the sacrifice of eigenfunctions realizes the theoretical goals of DMD analysis that have yet to be achieved in other contexts. However, in the case where the domain is embedded in the range, an eigenfunction approach is still achievable, where a more typical DMD routine is established, but that leverages a finite rank representation that converges in norm. The manuscript concludes with the description of two Dynamic Mode Decomposition algorithms that converges when a dense collection of occupation kernels, arising from the data, are leveraged in the analysis.

Anti-Koopmanism

This article addresses several longstanding misconceptions concerning Koopman operators, including the existence of lattices of eigenfunctions, common eigenfunctions between Koopman operators, and boundedness and compactness of Koopman operators, among others. Counterexamples are provided for each misconception. This manuscript also proves that the Gaussian RBF's native space only supports bounded Koopman operator corresponding to affine dynamics, which shows that the assumption of boundedness is very limiting. A framework for DMD is presented that requires only densely defined Koopman operators over reproducing kernel Hilbert spaces, and the effectiveness of this approach is demonstrated through reconstruction examples.

Control Occupation Kernel Regression for Nonlinear Control-Affine Systems

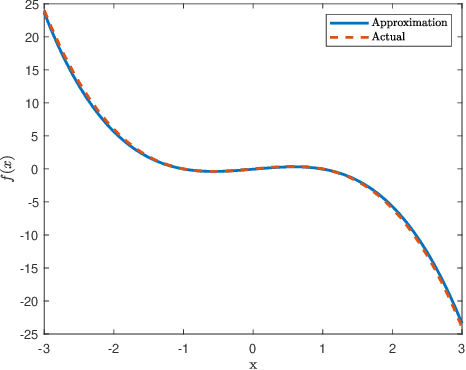
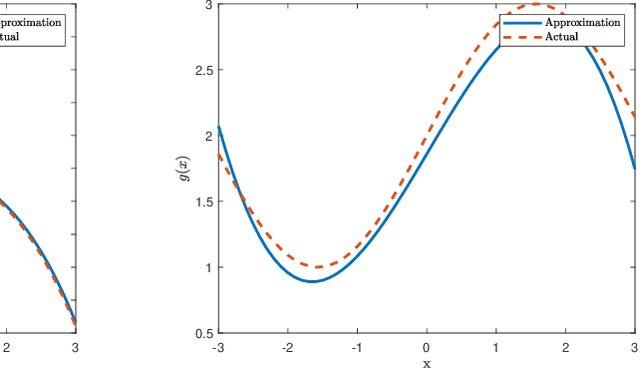
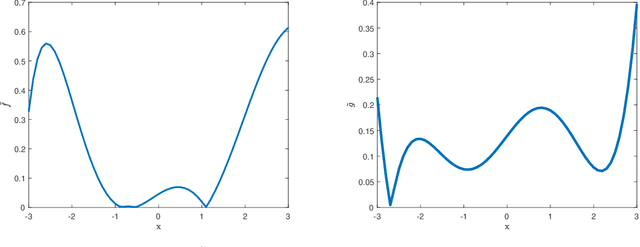
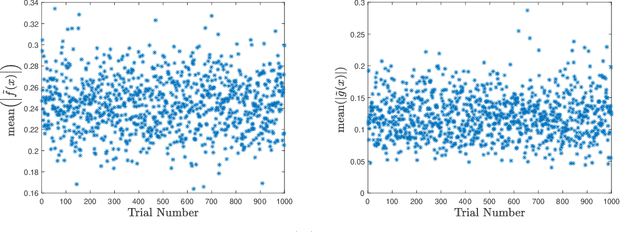
This manuscript presents an algorithm for obtaining an approximation of nonlinear high order control affine dynamical systems, that leverages the controlled trajectories as the central unit of information. As the fundamental basis elements leveraged in approximation, higher order control occupation kernels represent iterated integration after multiplication by a given controller in a vector valued reproducing kernel Hilbert space. In a regularized regression setting, the unique optimizer for a particular optimization problem is expressed as a linear combination of these occupation kernels, which converts an infinite dimensional optimization problem to a finite dimensional optimization problem through the representer theorem. Interestingly, the vector valued structure of the Hilbert space allows for simultaneous approximation of the drift and control effectiveness components of the control affine system. Several experiments are performed to demonstrate the effectiveness of the approach.

Online Observer-Based Inverse Reinforcement Learning

In this paper, a novel approach to the output-feedback inverse reinforcement learning (IRL) problem is developed by casting the IRL problem, for linear systems with quadratic cost functions, as a state estimation problem. Two observer-based techniques for IRL are developed, including a novel observer method that re-uses previous state estimates via history stacks. Theoretical guarantees for convergence and robustness are established under appropriate excitation conditions. Simulations demonstrate the performance of the developed observers and filters under noisy and noise-free measurements.

Extension of Full and Reduced Order Observers for Image-based Depth Estimation using Concurrent Learning

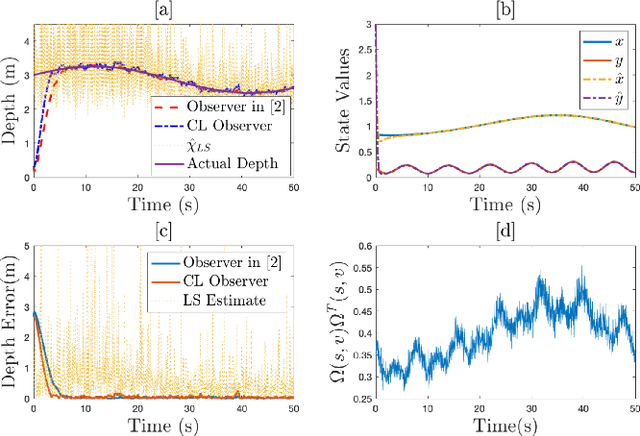
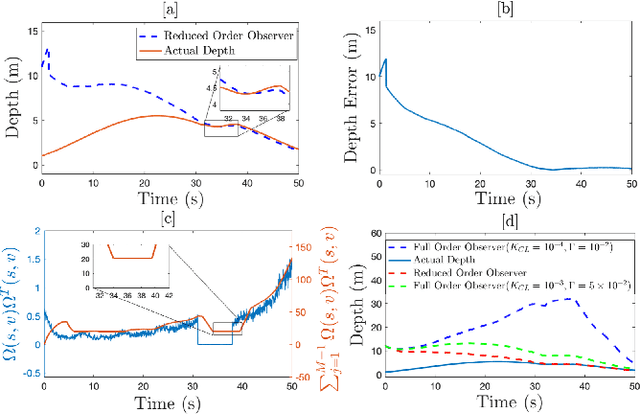
In this paper concurrent learning (CL)-based full and reduced order observers for a perspective dynamical system (PDS) are developed. The PDS is a widely used model for estimating the depth of a feature point from a sequence of camera images. Building on the current progress of CL for parameter estimation in adaptive control, a state observer is developed for the PDS model where the inverse depth appears as a time-varying parameter in the dynamics. The data recorded over a sliding time window in the near past is used in the CL term to design the full and the reduced order state observers. A Lyapunov-based stability analysis is carried out to prove the uniformly ultimately bounded (UUB) stability of the developed observers. Simulation results are presented to validate the accuracy and convergence of the developed observers in terms of convergence time, root mean square error (RMSE) and mean absolute percentage error (MAPE) metrics. Real world depth estimation experiments are performed to demonstrate the performance of the observers using aforementioned metrics on a 7-DoF manipulator with an eye-in-hand configuration.

Efficient model-based reinforcement learning for approximate online optimal

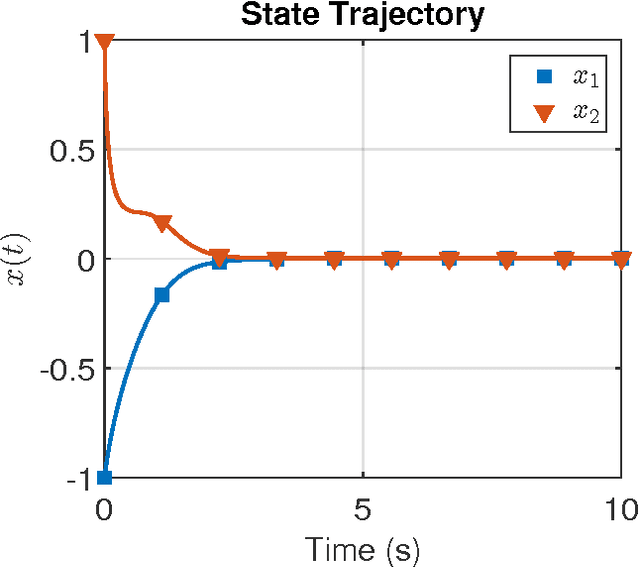
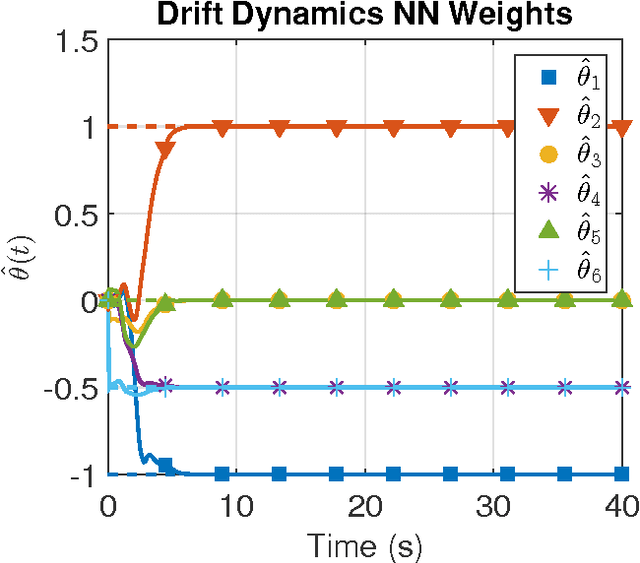
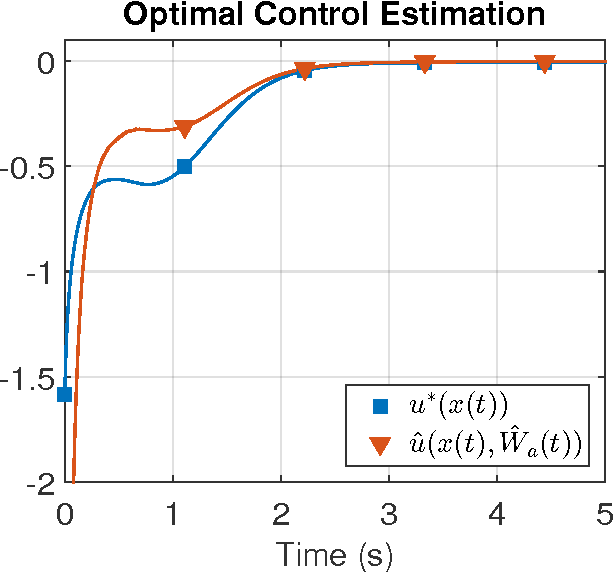
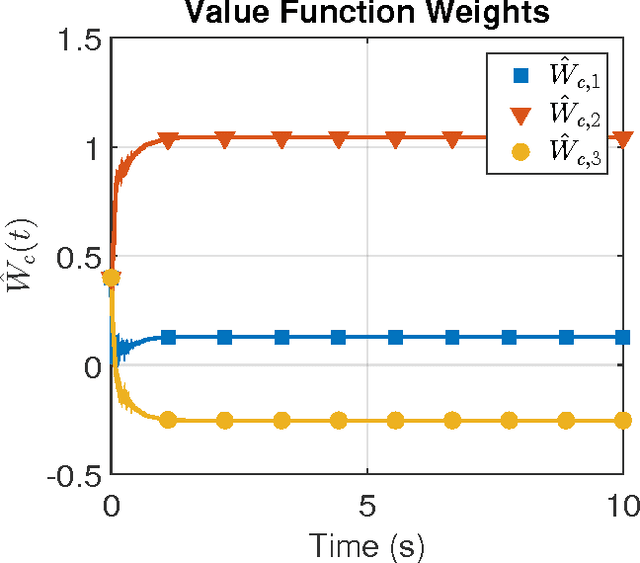
In this paper the infinite horizon optimal regulation problem is solved online for a deterministic control-affine nonlinear dynamical system using the state following (StaF) kernel method to approximate the value function. Unlike traditional methods that aim to approximate a function over a large compact set, the StaF kernel method aims to approximate a function in a small neighborhood of a state that travels within a compact set. Simulation results demonstrate that stability and approximate optimality of the control system can be achieved with significantly fewer basis functions than may be required for global approximation methods.