Singular Dynamic Mode Decompositions

This manuscript is aimed at addressing several long standing limitations of dynamic mode decompositions in the application of Koopman analysis. Principle among these limitations are the convergence of associated Dynamic Mode Decomposition algorithms and the existence of Koopman modes. To address these limitations, two major modifications are made, where Koopman operators are removed from the analysis in light of Liouville operators (known as Koopman generators in special cases), and these operators are shown to be compact for certain pairs of Hilbert spaces selected separately as the domain and range of the operator. While eigenfunctions are discarded in the general analysis, a viable reconstruction algorithm is still demonstrated, and the sacrifice of eigenfunctions realizes the theoretical goals of DMD analysis that have yet to be achieved in other contexts. However, in the case where the domain is embedded in the range, an eigenfunction approach is still achievable, where a more typical DMD routine is established, but that leverages a finite rank representation that converges in norm. The manuscript concludes with the description of two Dynamic Mode Decomposition algorithms that converges when a dense collection of occupation kernels, arising from the data, are leveraged in the analysis.

Anti-Koopmanism

This article addresses several longstanding misconceptions concerning Koopman operators, including the existence of lattices of eigenfunctions, common eigenfunctions between Koopman operators, and boundedness and compactness of Koopman operators, among others. Counterexamples are provided for each misconception. This manuscript also proves that the Gaussian RBF's native space only supports bounded Koopman operator corresponding to affine dynamics, which shows that the assumption of boundedness is very limiting. A framework for DMD is presented that requires only densely defined Koopman operators over reproducing kernel Hilbert spaces, and the effectiveness of this approach is demonstrated through reconstruction examples.

Control Occupation Kernel Regression for Nonlinear Control-Affine Systems

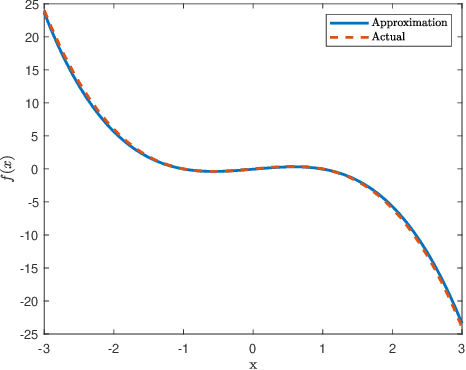
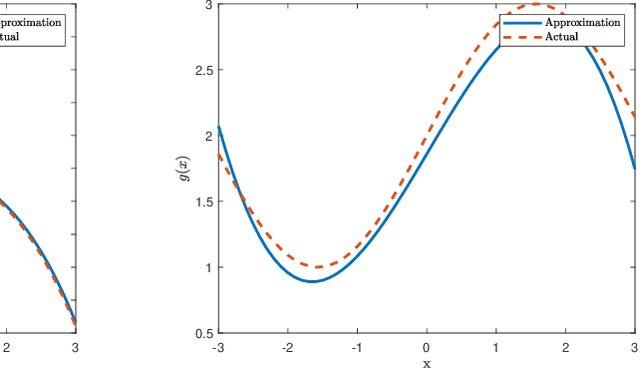
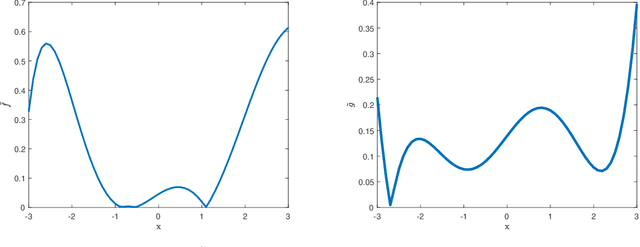
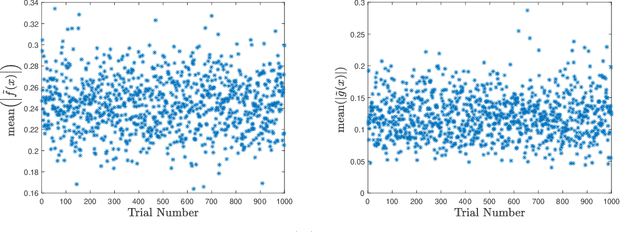
This manuscript presents an algorithm for obtaining an approximation of nonlinear high order control affine dynamical systems, that leverages the controlled trajectories as the central unit of information. As the fundamental basis elements leveraged in approximation, higher order control occupation kernels represent iterated integration after multiplication by a given controller in a vector valued reproducing kernel Hilbert space. In a regularized regression setting, the unique optimizer for a particular optimization problem is expressed as a linear combination of these occupation kernels, which converts an infinite dimensional optimization problem to a finite dimensional optimization problem through the representer theorem. Interestingly, the vector valued structure of the Hilbert space allows for simultaneous approximation of the drift and control effectiveness components of the control affine system. Several experiments are performed to demonstrate the effectiveness of the approach.

Occupation Kernel Hilbert Spaces and the Spectral Analysis of Nonlocal Operators

This manuscript introduces a space of functions, termed occupation kernel Hilbert space (OKHS), that operate on collections of signals rather than real or complex functions. To support this new definition, an explicit class of OKHSs is given through the consideration of a reproducing kernel Hilbert space (RKHS). This space enables the definition of nonlocal operators, such as fractional order Liouville operators, as well as spectral decomposition methods for corresponding fractional order dynamical systems. In this manuscript, a fractional order DMD routine is presented, and the details of the finite rank representations are given. Significantly, despite the added theoretical content through the OKHS formulation, the resultant computations only differ slightly from that of occupation kernel DMD methods for integer order systems posed over RKHSs.

Efficient model-based reinforcement learning for approximate online optimal

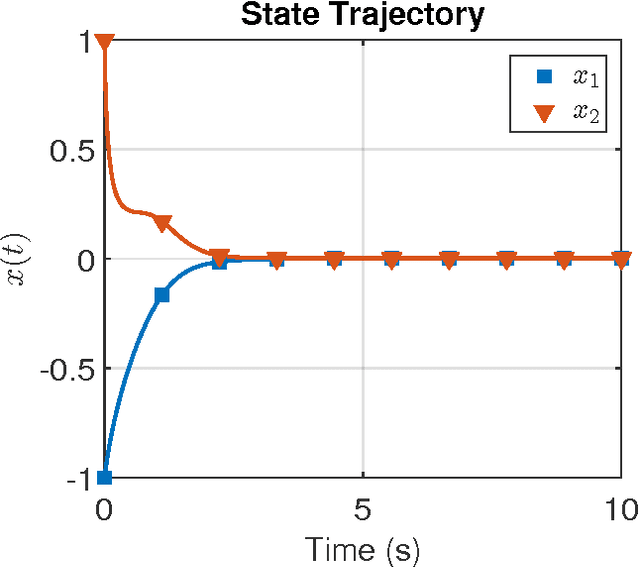
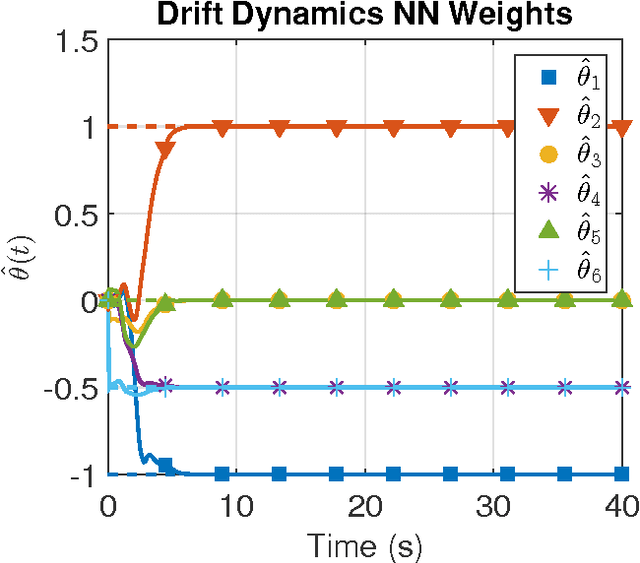
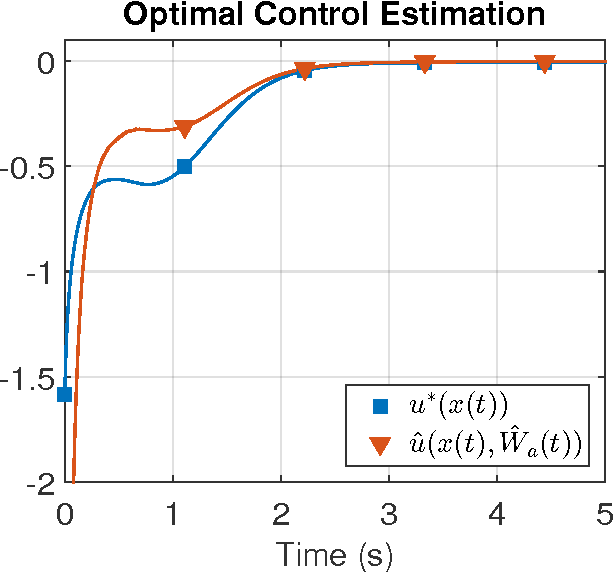
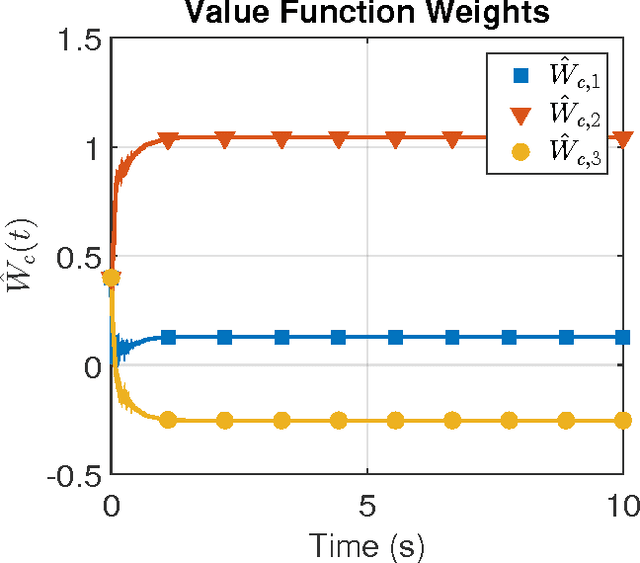
In this paper the infinite horizon optimal regulation problem is solved online for a deterministic control-affine nonlinear dynamical system using the state following (StaF) kernel method to approximate the value function. Unlike traditional methods that aim to approximate a function over a large compact set, the StaF kernel method aims to approximate a function in a small neighborhood of a state that travels within a compact set. Simulation results demonstrate that stability and approximate optimality of the control system can be achieved with significantly fewer basis functions than may be required for global approximation methods.