CXR-LanIC: Language-Grounded Interpretable Classifier for Chest X-Ray Diagnosis

Deep learning models have achieved remarkable accuracy in chest X-ray diagnosis, yet their widespread clinical adoption remains limited by the black-box nature of their predictions. Clinicians require transparent, verifiable explanations to trust automated diagnoses and identify potential failure modes. We introduce CXR-LanIC (Language-Grounded Interpretable Classifier for Chest X-rays), a novel framework that addresses this interpretability challenge through task-aligned pattern discovery. Our approach trains transcoder-based sparse autoencoders on a BiomedCLIP diagnostic classifier to decompose medical image representations into interpretable visual patterns. By training an ensemble of 100 transcoders on multimodal embeddings from the MIMIC-CXR dataset, we discover approximately 5,000 monosemantic patterns spanning cardiac, pulmonary, pleural, structural, device, and artifact categories. Each pattern exhibits consistent activation behavior across images sharing specific radiological features, enabling transparent attribution where predictions decompose into 20-50 interpretable patterns with verifiable activation galleries. CXR-LanIC achieves competitive diagnostic accuracy on five key findings while providing the foundation for natural language explanations through planned large multimodal model annotation. Our key innovation lies in extracting interpretable features from a classifier trained on specific diagnostic objectives rather than general-purpose embeddings, ensuring discovered patterns are directly relevant to clinical decision-making, demonstrating that medical AI systems can be both accurate and interpretable, supporting safer clinical deployment through transparent, clinically grounded explanations.

Representation Collapsing Problems in Vector Quantization

Vector quantization is a technique in machine learning that discretizes continuous representations into a set of discrete vectors. It is widely employed in tokenizing data representations for large language models, diffusion models, and other generative models. Despite its prevalence, the characteristics and behaviors of vector quantization in generative models remain largely underexplored. In this study, we investigate representation collapse in vector quantization - a critical degradation where codebook tokens or latent embeddings lose their discriminative power by converging to a limited subset of values. This collapse fundamentally compromises the model's ability to capture diverse data patterns. By leveraging both synthetic and real datasets, we identify the severity of each type of collapses and triggering conditions. Our analysis reveals that restricted initialization and limited encoder capacity result in tokens collapse and embeddings collapse. Building on these findings, we propose potential solutions aimed at mitigating each collapse. To the best of our knowledge, this is the first comprehensive study examining representation collapsing problems in vector quantization.

Improving Discrete Optimisation Via Decoupled Straight-Through Gumbel-Softmax

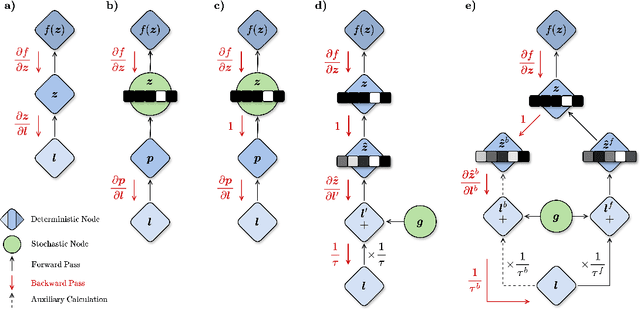
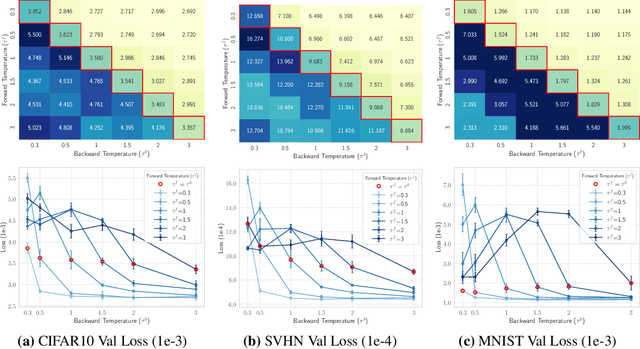
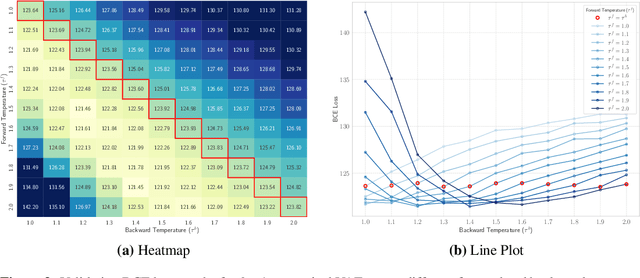
Discrete representations play a crucial role in many deep learning architectures, yet their non-differentiable nature poses significant challenges for gradient-based optimization. To address this issue, various gradient estimators have been developed, including the Straight-Through Gumbel-Softmax (ST-GS) estimator, which combines the Straight-Through Estimator (STE) and the Gumbel-based reparameterization trick. However, the performance of ST-GS is highly sensitive to temperature, with its selection often compromising gradient fidelity. In this work, we propose a simple yet effective extension to ST-GS by employing decoupled temperatures for forward and backward passes, which we refer to as "Decoupled ST-GS". We show that our approach significantly enhances the original ST-GS through extensive experiments across multiple tasks and datasets. We further investigate the impact of our method on gradient fidelity from multiple perspectives, including the gradient gap and the bias-variance trade-off of estimated gradients. Our findings contribute to the ongoing effort to improve discrete optimization in deep learning, offering a practical solution that balances simplicity and effectiveness.

Gaussian Mixture Vector Quantization with Aggregated Categorical Posterior

The vector quantization is a widely used method to map continuous representation to discrete space and has important application in tokenization for generative mode, bottlenecking information and many other tasks in machine learning. Vector Quantized Variational Autoencoder (VQ-VAE) is a type of variational autoencoder using discrete embedding as latent. We generalize the technique further, enriching the probabilistic framework with a Gaussian mixture as the underlying generative model. This framework leverages a codebook of latent means and adaptive variances to capture complex data distributions. This principled framework avoids various heuristics and strong assumptions that are needed with the VQ-VAE to address training instability and to improve codebook utilization. This approach integrates the benefits of both discrete and continuous representations within a variational Bayesian framework. Furthermore, by introducing the \textit{Aggregated Categorical Posterior Evidence Lower Bound} (ALBO), we offer a principled alternative optimization objective that aligns variational distributions with the generative model. Our experiments demonstrate that GM-VQ improves codebook utilization and reduces information loss without relying on handcrafted heuristics.