Improving Discrete Optimisation Via Decoupled Straight-Through Gumbel-Softmax
Paper and Code
Oct 17, 2024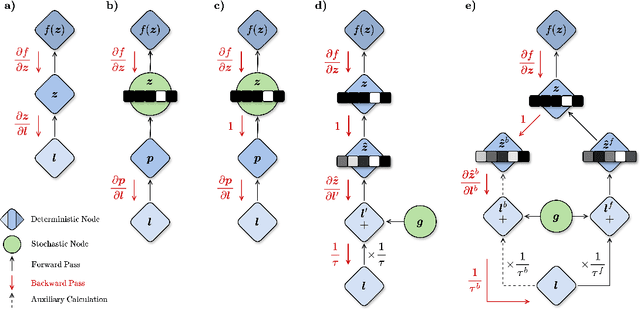

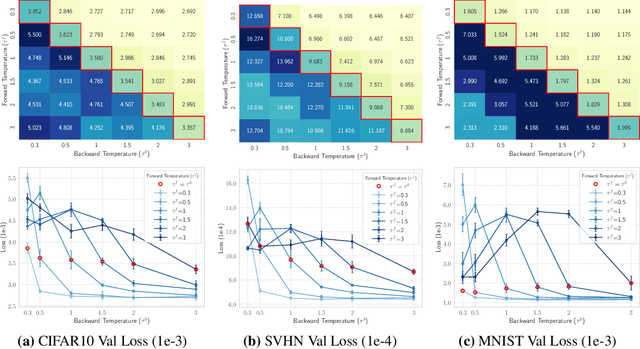
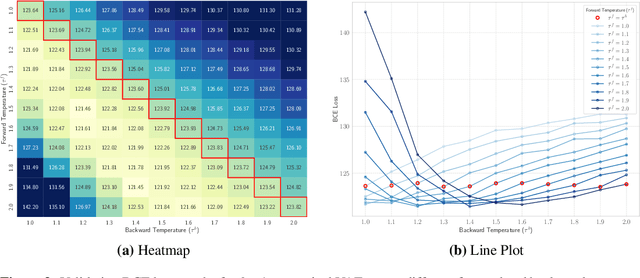
Discrete representations play a crucial role in many deep learning architectures, yet their non-differentiable nature poses significant challenges for gradient-based optimization. To address this issue, various gradient estimators have been developed, including the Straight-Through Gumbel-Softmax (ST-GS) estimator, which combines the Straight-Through Estimator (STE) and the Gumbel-based reparameterization trick. However, the performance of ST-GS is highly sensitive to temperature, with its selection often compromising gradient fidelity. In this work, we propose a simple yet effective extension to ST-GS by employing decoupled temperatures for forward and backward passes, which we refer to as "Decoupled ST-GS". We show that our approach significantly enhances the original ST-GS through extensive experiments across multiple tasks and datasets. We further investigate the impact of our method on gradient fidelity from multiple perspectives, including the gradient gap and the bias-variance trade-off of estimated gradients. Our findings contribute to the ongoing effort to improve discrete optimization in deep learning, offering a practical solution that balances simplicity and effectiveness.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge