The Impact of Feature Causality on Normal Behaviour Models for SCADA-based Wind Turbine Fault Detection

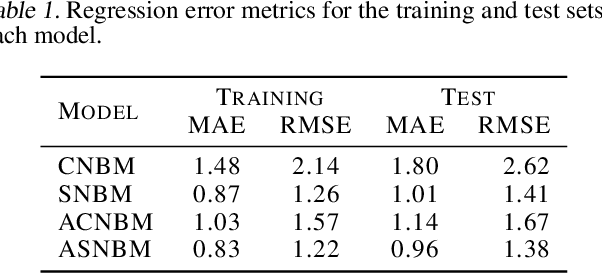
The cost of wind energy can be reduced by using SCADA data to detect faults in wind turbine components. Normal behavior models are one of the main fault detection approaches, but there is a lack of consensus in how different input features affect the results. In this work, a new taxonomy based on the causal relations between the input features and the target is presented. Based on this taxonomy, the impact of different input feature configurations on the modelling and fault detection performance is evaluated. To this end, a framework that formulates the detection of faults as a classification problem is also presented.

Joint Optimization and Variable Selection of High-dimensional Gaussian Processes

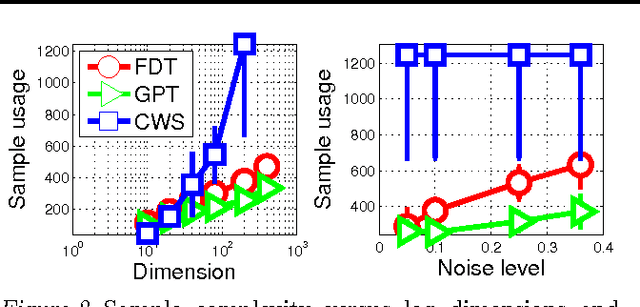
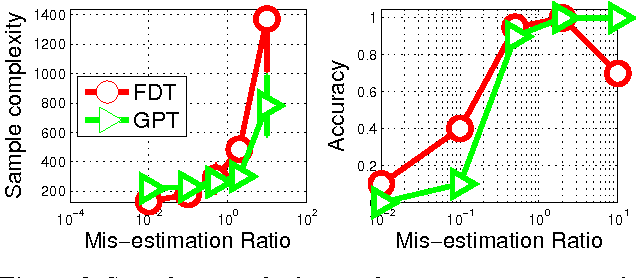
Maximizing high-dimensional, non-convex functions through noisy observations is a notoriously hard problem, but one that arises in many applications. In this paper, we tackle this challenge by modeling the unknown function as a sample from a high-dimensional Gaussian process (GP) distribution. Assuming that the unknown function only depends on few relevant variables, we show that it is possible to perform joint variable selection and GP optimization. We provide strong performance guarantees for our algorithm, bounding the sample complexity of variable selection, and as well as providing cumulative regret bounds. We further provide empirical evidence on the effectiveness of our algorithm on several benchmark optimization problems.

Distilled Sensing: Adaptive Sampling for Sparse Detection and Estimation

Adaptive sampling results in dramatic improvements in the recovery of sparse signals in white Gaussian noise. A sequential adaptive sampling-and-refinement procedure called Distilled Sensing (DS) is proposed and analyzed. DS is a form of multi-stage experimental design and testing. Because of the adaptive nature of the data collection, DS can detect and localize far weaker signals than possible from non-adaptive measurements. In particular, reliable detection and localization (support estimation) using non-adaptive samples is possible only if the signal amplitudes grow logarithmically with the problem dimension. Here it is shown that using adaptive sampling, reliable detection is possible provided the amplitude exceeds a constant, and localization is possible when the amplitude exceeds any arbitrarily slowly growing function of the dimension.