A Fast Quartet Tree Heuristic for Hierarchical Clustering

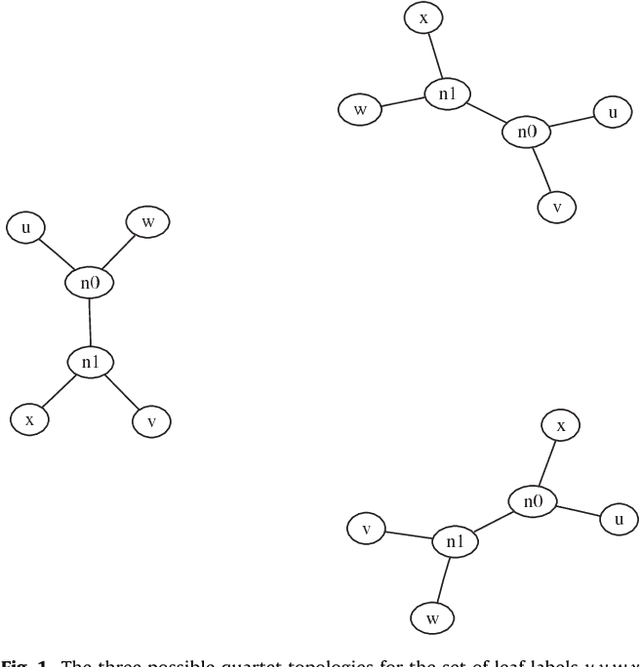
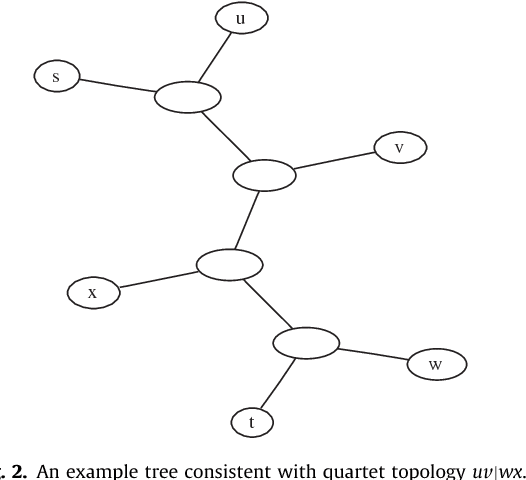
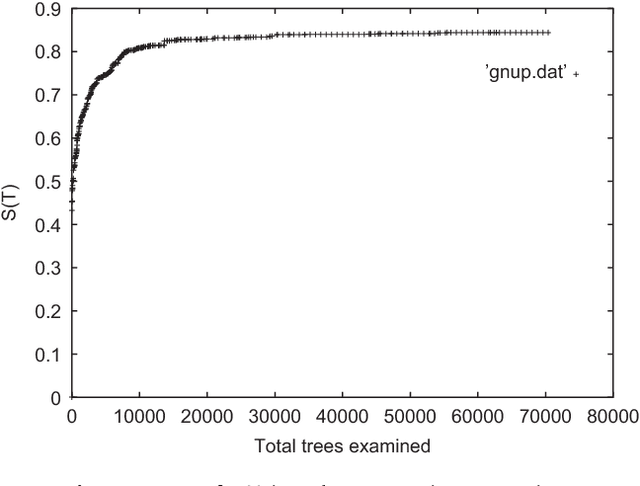
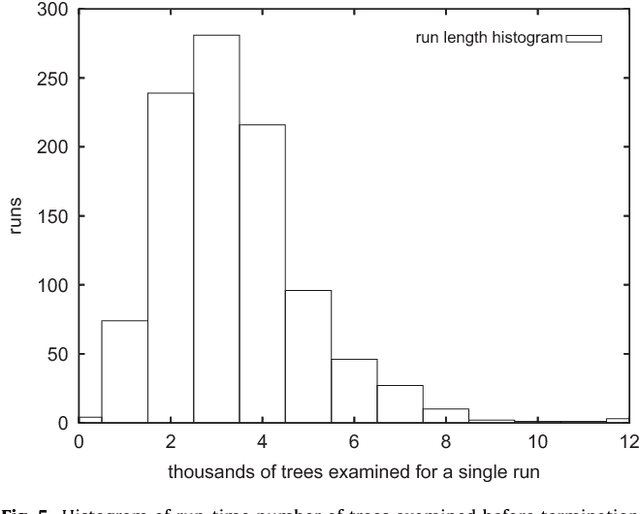
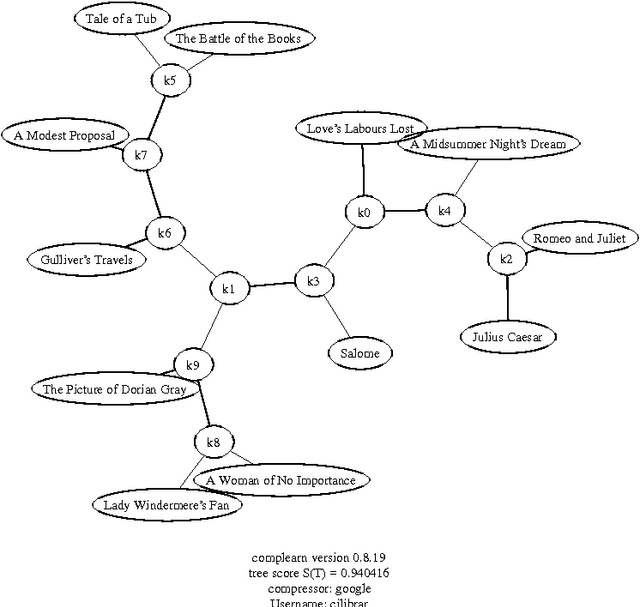
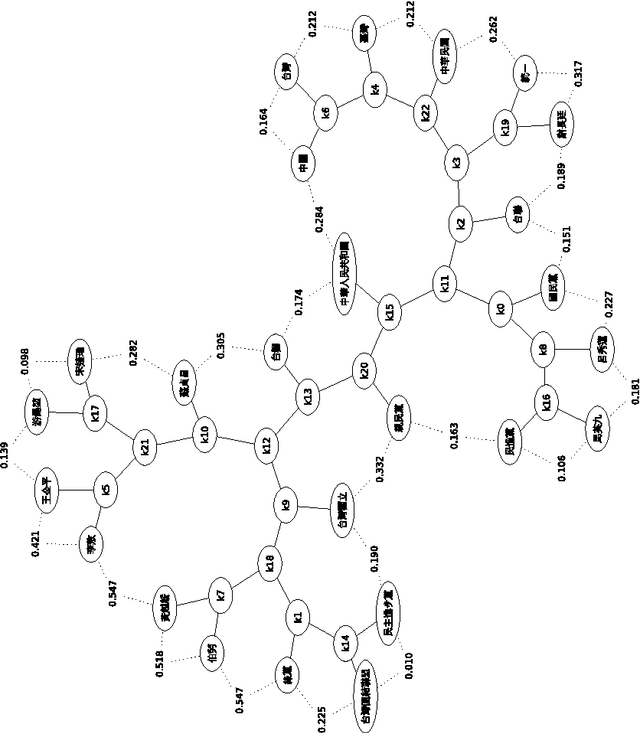
The Minimum Quartet Tree Cost problem is to construct an optimal weight tree from the $3{n \choose 4}$ weighted quartet topologies on $n$ objects, where optimality means that the summed weight of the embedded quartet topologies is optimal (so it can be the case that the optimal tree embeds all quartets as nonoptimal topologies). We present a Monte Carlo heuristic, based on randomized hill climbing, for approximating the optimal weight tree, given the quartet topology weights. The method repeatedly transforms a dendrogram, with all objects involved as leaves, achieving a monotonic approximation to the exact single globally optimal tree. The problem and the solution heuristic has been extensively used for general hierarchical clustering of nontree-like (non-phylogeny) data in various domains and across domains with heterogeneous data. We also present a greatly improved heuristic, reducing the running time by a factor of order a thousand to ten thousand. All this is implemented and available, as part of the CompLearn package. We compare performance and running time of the original and improved versions with those of UPGMA, BioNJ, and NJ, as implemented in the SplitsTree package on genomic data for which the latter are optimized. Keywords: Data and knowledge visualization, Pattern matching--Clustering--Algorithms/Similarity measures, Hierarchical clustering, Global optimization, Quartet tree, Randomized hill-climbing,

Normalized Web Distance and Word Similarity

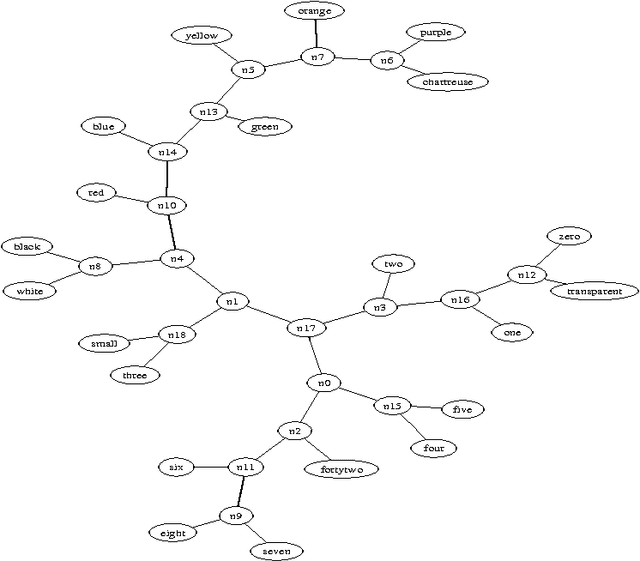
There is a great deal of work in cognitive psychology, linguistics, and computer science, about using word (or phrase) frequencies in context in text corpora to develop measures for word similarity or word association, going back to at least the 1960s. The goal of this chapter is to introduce the normalizedis a general way to tap the amorphous low-grade knowledge available for free on the Internet, typed in by local users aiming at personal gratification of diverse objectives, and yet globally achieving what is effectively the largest semantic electronic database in the world. Moreover, this database is available for all by using any search engine that can return aggregate page-count estimates for a large range of search-queries. In the paper introducing the NWD it was called `normalized Google distance (NGD),' but since Google doesn't allow computer searches anymore, we opt for the more neutral and descriptive NWD. web distance (NWD) method to determine similarity between words and phrases. It

Normalized Information Distance

The normalized information distance is a universal distance measure for objects of all kinds. It is based on Kolmogorov complexity and thus uncomputable, but there are ways to utilize it. First, compression algorithms can be used to approximate the Kolmogorov complexity if the objects have a string representation. Second, for names and abstract concepts, page count statistics from the World Wide Web can be used. These practical realizations of the normalized information distance can then be applied to machine learning tasks, expecially clustering, to perform feature-free and parameter-free data mining. This chapter discusses the theoretical foundations of the normalized information distance and both practical realizations. It presents numerous examples of successful real-world applications based on these distance measures, ranging from bioinformatics to music clustering to machine translation.