Identification of Probabilities

Within psychology, neuroscience and artificial intelligence, there has been increasing interest in the proposal that the brain builds probabilistic models of sensory and linguistic input: that is, to infer a probabilistic model from a sample. The practical problems of such inference are substantial: the brain has limited data and restricted computational resources. But there is a more fundamental question: is the problem of inferring a probabilistic model from a sample possible even in principle? We explore this question and find some surprisingly positive and general results. First, for a broad class of probability distributions characterised by computability restrictions, we specify a learning algorithm that will almost surely identify a probability distribution in the limit given a finite i.i.d. sample of sufficient but unknown length. This is similarly shown to hold for sequences generated by a broad class of Markov chains, subject to computability assumptions. The technical tool is the strong law of large numbers. Second, for a large class of dependent sequences, we specify an algorithm which identifies in the limit a computable measure for which the sequence is typical, in the sense of Martin-Lof (there may be more than one such measure). The technical tool is the theory of Kolmogorov complexity. We analyse the associated predictions in both cases. We also briefly consider special cases, including language learning, and wider theoretical implications for psychology.

Web Similarity

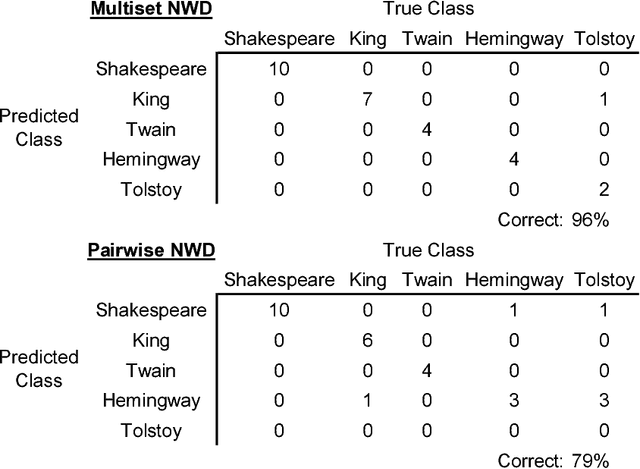
Normalized web distance (NWD) is a similarity or normalized semantic distance based on the World Wide Web or any other large electronic database, for instance Wikipedia, and a search engine that returns reliable aggregate page counts. For sets of search terms the NWD gives a similarity on a scale from 0 (identical) to 1 (completely different). The NWD approximates the similarity according to all (upper semi)computable properties. We develop the theory and give applications. The derivation of the NWD method is based on Kolmogorov complexity.

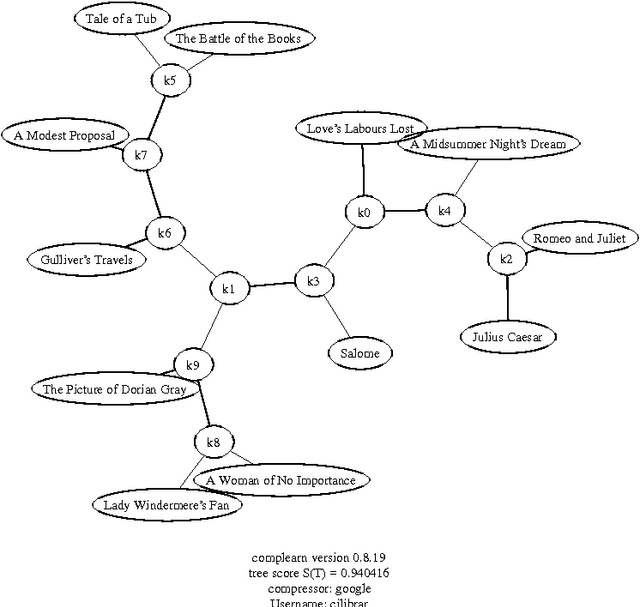
A Fast Quartet Tree Heuristic for Hierarchical Clustering

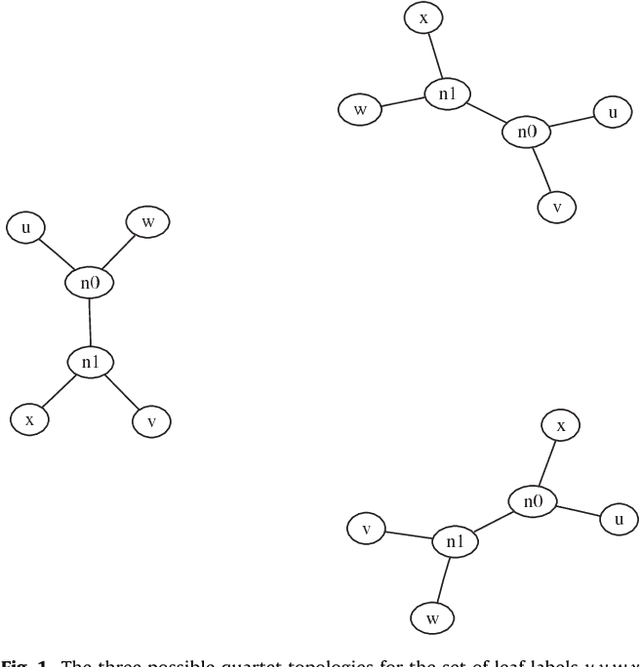
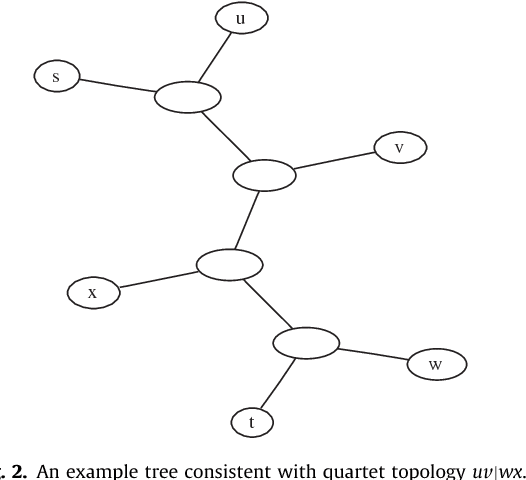
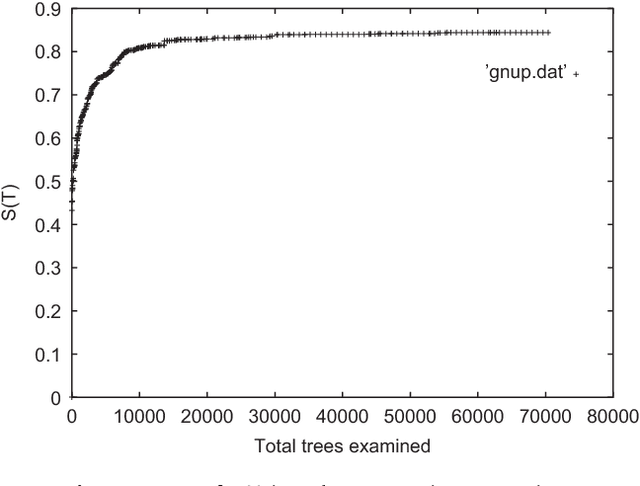
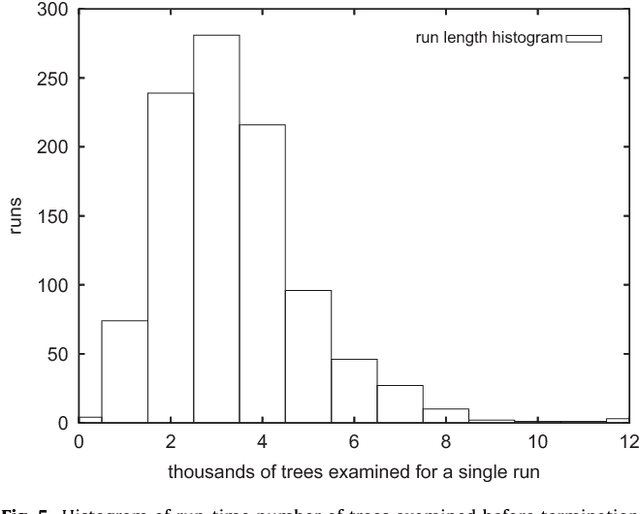
The Minimum Quartet Tree Cost problem is to construct an optimal weight tree from the $3{n \choose 4}$ weighted quartet topologies on $n$ objects, where optimality means that the summed weight of the embedded quartet topologies is optimal (so it can be the case that the optimal tree embeds all quartets as nonoptimal topologies). We present a Monte Carlo heuristic, based on randomized hill climbing, for approximating the optimal weight tree, given the quartet topology weights. The method repeatedly transforms a dendrogram, with all objects involved as leaves, achieving a monotonic approximation to the exact single globally optimal tree. The problem and the solution heuristic has been extensively used for general hierarchical clustering of nontree-like (non-phylogeny) data in various domains and across domains with heterogeneous data. We also present a greatly improved heuristic, reducing the running time by a factor of order a thousand to ten thousand. All this is implemented and available, as part of the CompLearn package. We compare performance and running time of the original and improved versions with those of UPGMA, BioNJ, and NJ, as implemented in the SplitsTree package on genomic data for which the latter are optimized. Keywords: Data and knowledge visualization, Pattern matching--Clustering--Algorithms/Similarity measures, Hierarchical clustering, Global optimization, Quartet tree, Randomized hill-climbing,

Identification of Probabilities of Languages

We consider the problem of inferring the probability distribution associated with a language, given data consisting of an infinite sequence of elements of the languge. We do this under two assumptions on the algorithms concerned: (i) like a real-life algorothm it has round-off errors, and (ii) it has no round-off errors. Assuming (i) we (a) consider a probability mass function of the elements of the language if the data are drawn independent identically distributed (i.i.d.), provided the probability mass function is computable and has a finite expectation. We give an effective procedure to almost surely identify in the limit the target probability mass function using the Strong Law of Large Numbers. Second (b) we treat the case of possibly incomputable probabilistic mass functions in the above setting. In this case we can only pointswize converge to the target probability mass function almost surely. Third (c) we consider the case where the data are dependent assuming they are typical for at least one computable measure and the language is finite. There is an effective procedure to identify by infinite recurrence a nonempty subset of the computable measures according to which the data is typical. Here we use the theory of Kolmogorov complexity. Assuming (ii) we obtain the weaker result for (a) that the target distribution is identified by infinite recurrence almost surely; (b) stays the same as under assumption (i). We consider the associated predictions.

Algorithmic Identification of Probabilities

TThe problem is to identify a probability associated with a set of natural numbers, given an infinite data sequence of elements from the set. If the given sequence is drawn i.i.d. and the probability mass function involved (the target) belongs to a computably enumerable (c.e.) or co-computably enumerable (co-c.e.) set of computable probability mass functions, then there is an algorithm to almost surely identify the target in the limit. The technical tool is the strong law of large numbers. If the set is finite and the elements of the sequence are dependent while the sequence is typical in the sense of Martin-L\"of for at least one measure belonging to a c.e. or co-c.e. set of computable measures, then there is an algorithm to identify in the limit a computable measure for which the sequence is typical (there may be more than one such measure). The technical tool is the theory of Kolmogorov complexity. We give the algorithms and consider the associated predictions.

Normalized Compression Distance of Multisets with Applications

Normalized compression distance (NCD) is a parameter-free, feature-free, alignment-free, similarity measure between a pair of finite objects based on compression. However, it is not sufficient for all applications. We propose an NCD of finite multisets (a.k.a. multiples) of finite objects that is also a metric. Previously, attempts to obtain such an NCD failed. We cover the entire trajectory from theoretical underpinning to feasible practice. The new NCD for multisets is applied to retinal progenitor cell classification questions and to related synthetically generated data that were earlier treated with the pairwise NCD. With the new method we achieved significantly better results. Similarly for questions about axonal organelle transport. We also applied the new NCD to handwritten digit recognition and improved classification accuracy significantly over that of pairwise NCD by incorporating both the pairwise and NCD for multisets. In the analysis we use the incomputable Kolmogorov complexity that for practical purposes is approximated from above by the length of the compressed version of the file involved, using a real-world compression program. Index Terms--- Normalized compression distance, multisets or multiples, pattern recognition, data mining, similarity, classification, Kolmogorov complexity, retinal progenitor cells, synthetic data, organelle transport, handwritten character recognition

Normalized Information Distance is Not Semicomputable

Normalized information distance (NID) uses the theoretical notion of Kolmogorov complexity, which for practical purposes is approximated by the length of the compressed version of the file involved, using a real-world compression program. This practical application is called 'normalized compression distance' and it is trivially computable. It is a parameter-free similarity measure based on compression, and is used in pattern recognition, data mining, phylogeny, clustering, and classification. The complexity properties of its theoretical precursor, the NID, have been open. We show that the NID is neither upper semicomputable nor lower semicomputable.

The probabilistic analysis of language acquisition: Theoretical, computational, and experimental analysis

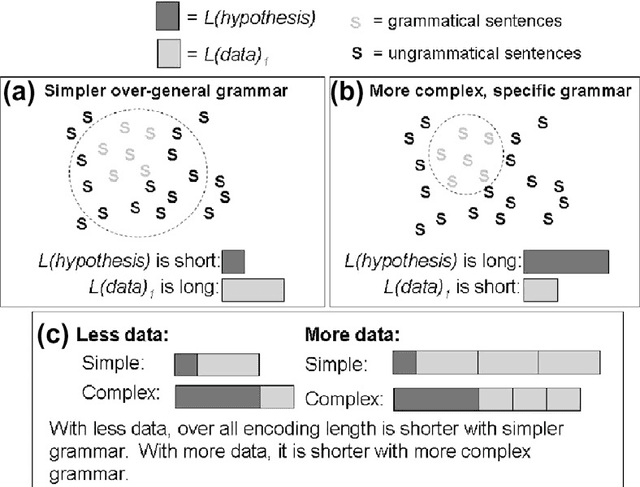
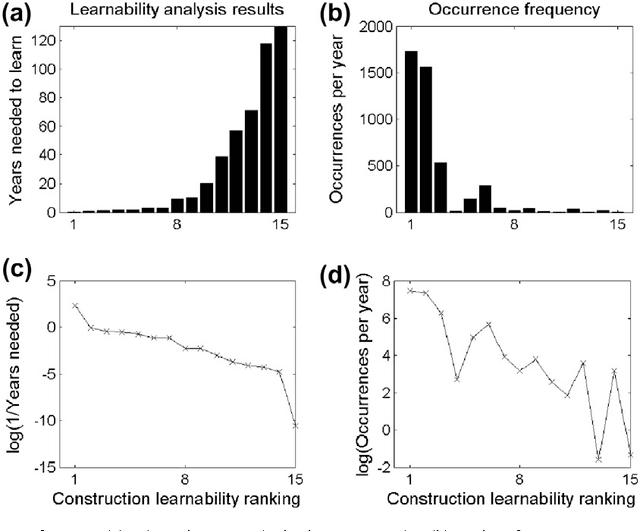
There is much debate over the degree to which language learning is governed by innate language-specific biases, or acquired through cognition-general principles. Here we examine the probabilistic language acquisition hypothesis on three levels: We outline a novel theoretical result showing that it is possible to learn the exact generative model underlying a wide class of languages, purely from observing samples of the language. We then describe a recently proposed practical framework, which quantifies natural language learnability, allowing specific learnability predictions to be made for the first time. In previous work, this framework was used to make learnability predictions for a wide variety of linguistic constructions, for which learnability has been much debated. Here, we present a new experiment which tests these learnability predictions. We find that our experimental results support the possibility that these linguistic constructions are acquired probabilistically from cognition-general principles.

Normalized Web Distance and Word Similarity

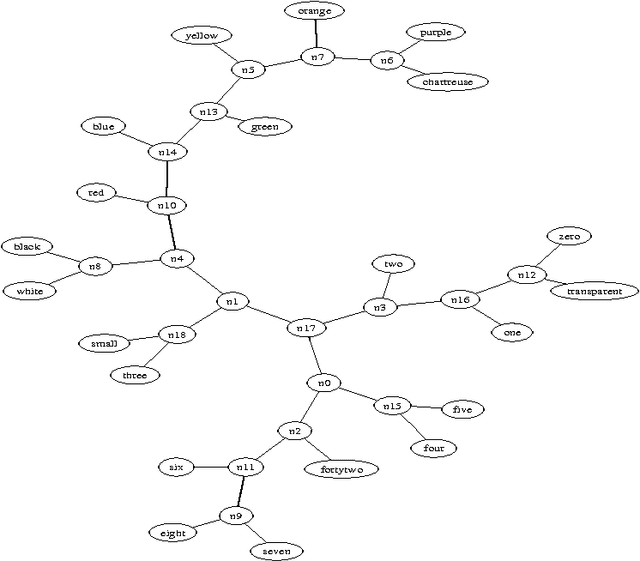
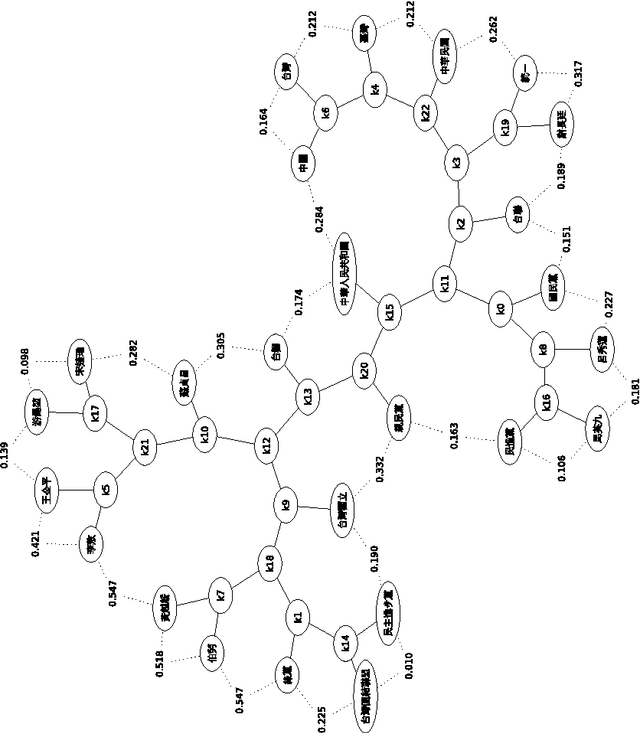
There is a great deal of work in cognitive psychology, linguistics, and computer science, about using word (or phrase) frequencies in context in text corpora to develop measures for word similarity or word association, going back to at least the 1960s. The goal of this chapter is to introduce the normalizedis a general way to tap the amorphous low-grade knowledge available for free on the Internet, typed in by local users aiming at personal gratification of diverse objectives, and yet globally achieving what is effectively the largest semantic electronic database in the world. Moreover, this database is available for all by using any search engine that can return aggregate page-count estimates for a large range of search-queries. In the paper introducing the NWD it was called `normalized Google distance (NGD),' but since Google doesn't allow computer searches anymore, we opt for the more neutral and descriptive NWD. web distance (NWD) method to determine similarity between words and phrases. It

Information Distance in Multiples

Information distance is a parameter-free similarity measure based on compression, used in pattern recognition, data mining, phylogeny, clustering, and classification. The notion of information distance is extended from pairs to multiples (finite lists). We study maximal overlap, metricity, universality, minimal overlap, additivity, and normalized information distance in multiples. We use the theoretical notion of Kolmogorov complexity which for practical purposes is approximated by the length of the compressed version of the file involved, using a real-world compression program. {\em Index Terms}-- Information distance, multiples, pattern recognition, data mining, similarity, Kolmogorov complexity