A Fast Quartet Tree Heuristic for Hierarchical Clustering

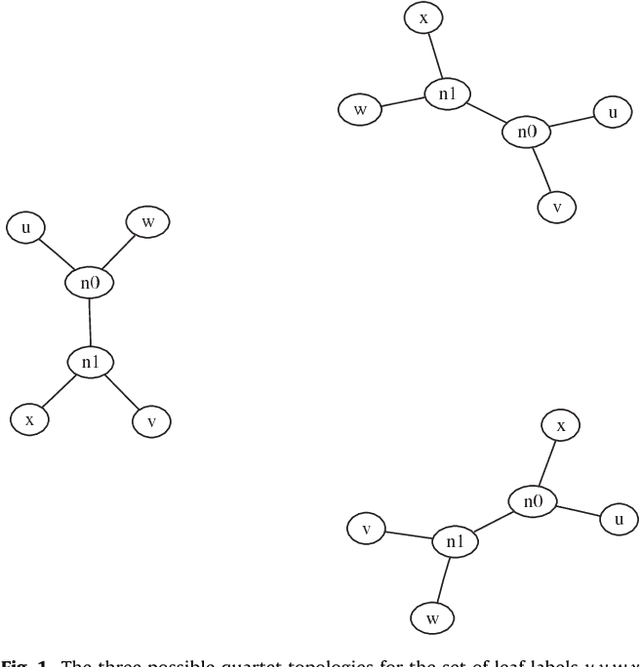
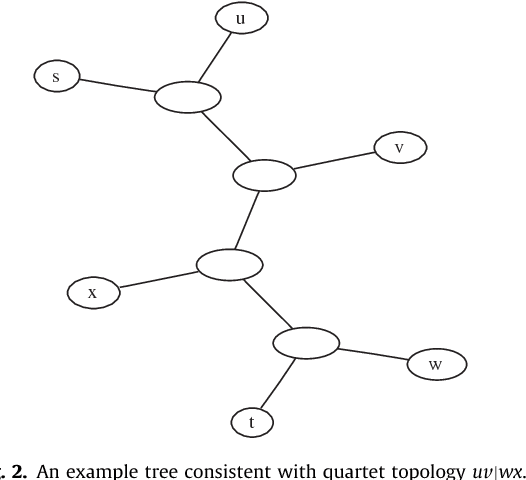
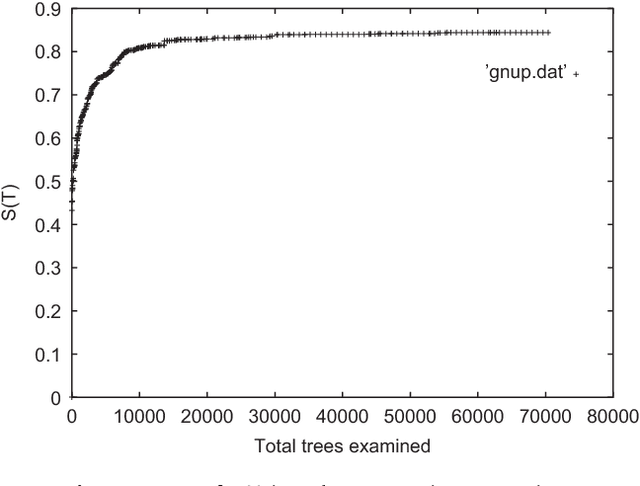
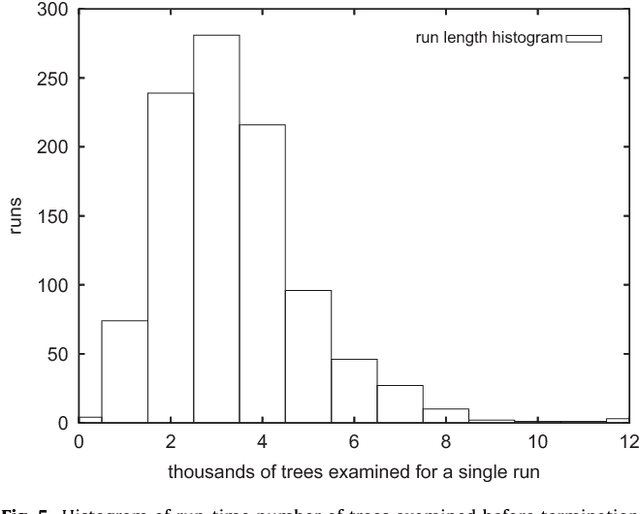
The Minimum Quartet Tree Cost problem is to construct an optimal weight tree from the $3{n \choose 4}$ weighted quartet topologies on $n$ objects, where optimality means that the summed weight of the embedded quartet topologies is optimal (so it can be the case that the optimal tree embeds all quartets as nonoptimal topologies). We present a Monte Carlo heuristic, based on randomized hill climbing, for approximating the optimal weight tree, given the quartet topology weights. The method repeatedly transforms a dendrogram, with all objects involved as leaves, achieving a monotonic approximation to the exact single globally optimal tree. The problem and the solution heuristic has been extensively used for general hierarchical clustering of nontree-like (non-phylogeny) data in various domains and across domains with heterogeneous data. We also present a greatly improved heuristic, reducing the running time by a factor of order a thousand to ten thousand. All this is implemented and available, as part of the CompLearn package. We compare performance and running time of the original and improved versions with those of UPGMA, BioNJ, and NJ, as implemented in the SplitsTree package on genomic data for which the latter are optimized. Keywords: Data and knowledge visualization, Pattern matching--Clustering--Algorithms/Similarity measures, Hierarchical clustering, Global optimization, Quartet tree, Randomized hill-climbing,