Algorithmic statistics of retinal images

There has been a tremendous amount of image processing and machine learning research to measure and classify disease progression from live optical coherence tomography (OCT) imaging of the retina. The images considered here are large, complex, three-dimensional (3-D) and difficult to visualize effectively. Many current supervised machine learning approaches, \emph{e.g.} neural networks, are non-metric meaning that any features or measurements generated can introduce systematic distortion that may be correlated with underlying non-meaningful physiological differences. Here we present a metric learning approach using the normalized compression distance (NCD) combined with anisotropic structure-enhancing filters to quantify and visualize the principal differences among a collection of 3-D retinal images. We validate the NCD-measured structural differences between pairs of images against the physician-measured change in visual field function, achieving a prediction error of $\sim$ 0.5 dB, more accurate than non-metric deep learning approaches. The normalized compression vectors (NCV) are proposed as a feature set measuring visual differences among a collection of 3-D microscopy images. The utility of the NCV for visualizing and measuring patterns of change is demonstrated for a human with moderate non-progressing glaucoma and for a non-human primate model using intraocular pressure setting manipulation. We conclude with a brief simulation of non-metric embedding features, \emph{e.g.} from neural networks, introducing class-correlated statistical distortion.

The cell signaling structure function

Live cell microscopy captures 5-D $(x,y,z,channel,time)$ movies that display patterns of cellular motion and signaling dynamics. We present here an approach to finding spatiotemporal patterns of cell signaling dynamics in 5-D live cell microscopy movies unique in requiring no a priori knowledge of expected pattern dynamics, and no training data. The proposed cell signaling structure function (SSF) is a Kolmogorov structure function that optimally measures cell signaling state as nuclear intensity w.r.t. surrounding cytoplasm, a significant improvement compared to the current state-of-the-art cytonuclear ratio. SSF kymographs store at each spatiotemporal cell centroid the SSF value, or a functional output such as velocity. Patterns of similarity are identified via the metric normalized compression distance (NCD). The NCD is a reproducing kernel for a Hilbert space that represents the input SSF kymographs as points in a low dimensional embedding that optimally captures the pattern similarity identified by the NCD throughout the space. The only parameter is the expected cell radii ($\mu m$). A new formulation of the cluster structure function optimally estimates how meaningful an embedding from the RKHS representation. Results are presented quantifying the impact of ERK and AKT signaling between different oncogenic mutations, and by the relation between ERK signaling and cellular velocity patterns for movies of 2-D monolayers of human breast epithelial (MCF10A) cells, 3-D MCF10A spheroids under optogenetic manipulation of ERK, and human induced pluripotent stem cells .

The cluster structure function

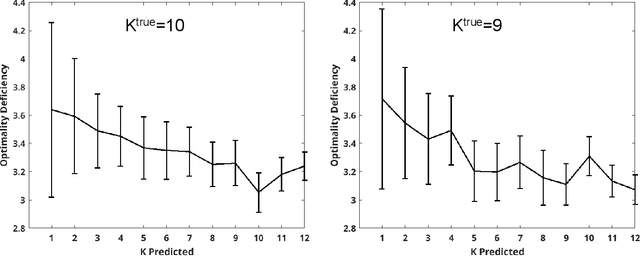
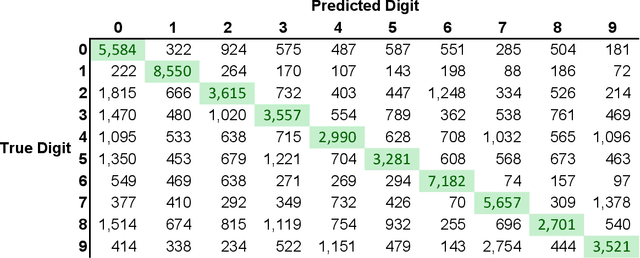
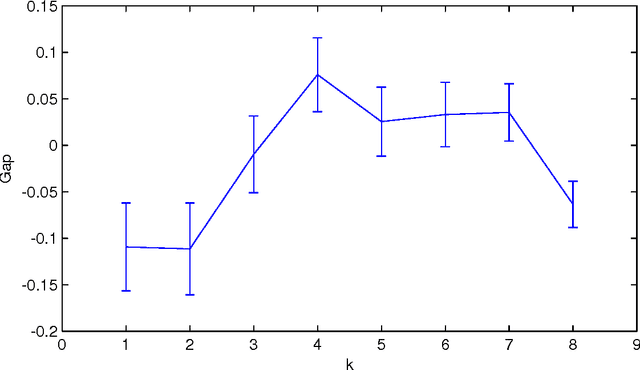
For each partition of a data set into a given number of parts there is a partition such that every part is as much as possible a good model (an "algorithmic sufficient statistic") for the data in that part. Since this can be done for every number between one and the number of data, the result is a function, the cluster structure function. It maps the number of parts of a partition to values related to the deficiencies of being good models by the parts. Such a function starts with a value at least zero for no partition of the data set and descents to zero for the partition of the data set into singleton parts. The optimal clustering is the one chosen to minimize the cluster structure function. The theory behind the method is expressed in algorithmic information theory (Kolmogorov complexity). In practice the Kolmogorov complexities involved are approximated by a concrete compressor. We give examples using real data sets: the MNIST handwritten digits and the segmentation of real cells as used in stem cell research.

Web Similarity

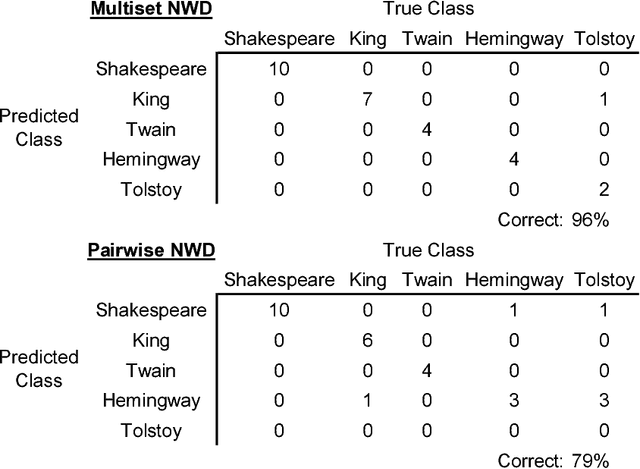
Normalized web distance (NWD) is a similarity or normalized semantic distance based on the World Wide Web or any other large electronic database, for instance Wikipedia, and a search engine that returns reliable aggregate page counts. For sets of search terms the NWD gives a similarity on a scale from 0 (identical) to 1 (completely different). The NWD approximates the similarity according to all (upper semi)computable properties. We develop the theory and give applications. The derivation of the NWD method is based on Kolmogorov complexity.

Normalized Google Distance of Multisets with Applications

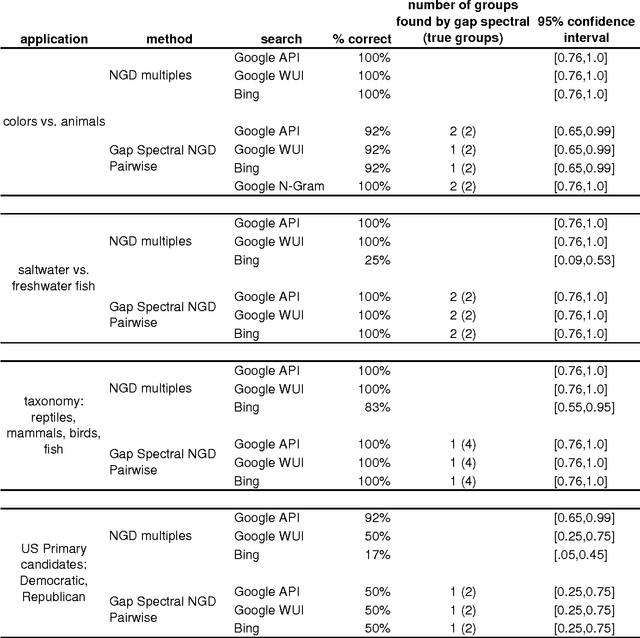
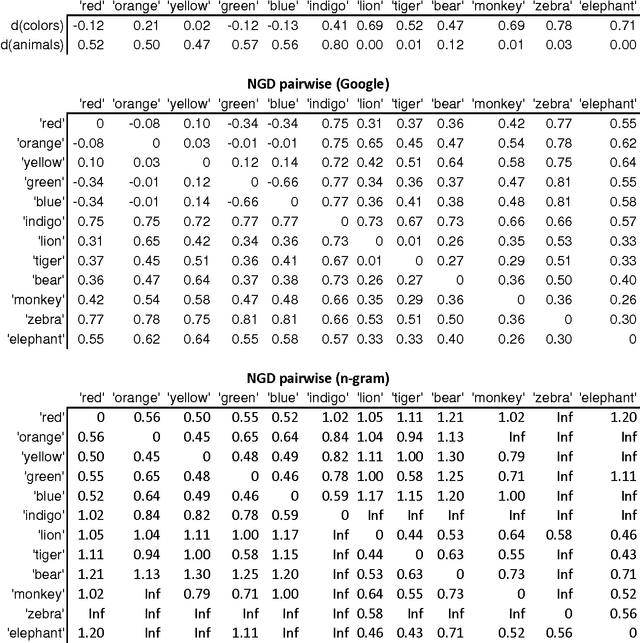
Normalized Google distance (NGD) is a relative semantic distance based on the World Wide Web (or any other large electronic database, for instance Wikipedia) and a search engine that returns aggregate page counts. The earlier NGD between pairs of search terms (including phrases) is not sufficient for all applications. We propose an NGD of finite multisets of search terms that is better for many applications. This gives a relative semantics shared by a multiset of search terms. We give applications and compare the results with those obtained using the pairwise NGD. The derivation of NGD method is based on Kolmogorov complexity.

Normalized Compression Distance of Multisets with Applications

Normalized compression distance (NCD) is a parameter-free, feature-free, alignment-free, similarity measure between a pair of finite objects based on compression. However, it is not sufficient for all applications. We propose an NCD of finite multisets (a.k.a. multiples) of finite objects that is also a metric. Previously, attempts to obtain such an NCD failed. We cover the entire trajectory from theoretical underpinning to feasible practice. The new NCD for multisets is applied to retinal progenitor cell classification questions and to related synthetically generated data that were earlier treated with the pairwise NCD. With the new method we achieved significantly better results. Similarly for questions about axonal organelle transport. We also applied the new NCD to handwritten digit recognition and improved classification accuracy significantly over that of pairwise NCD by incorporating both the pairwise and NCD for multisets. In the analysis we use the incomputable Kolmogorov complexity that for practical purposes is approximated from above by the length of the compressed version of the file involved, using a real-world compression program. Index Terms--- Normalized compression distance, multisets or multiples, pattern recognition, data mining, similarity, classification, Kolmogorov complexity, retinal progenitor cells, synthetic data, organelle transport, handwritten character recognition