The cluster structure function

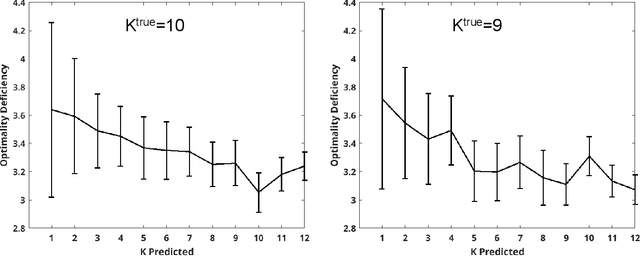
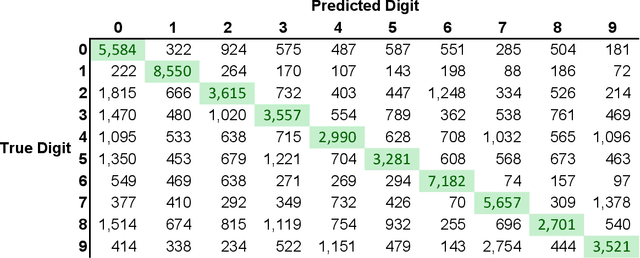
For each partition of a data set into a given number of parts there is a partition such that every part is as much as possible a good model (an "algorithmic sufficient statistic") for the data in that part. Since this can be done for every number between one and the number of data, the result is a function, the cluster structure function. It maps the number of parts of a partition to values related to the deficiencies of being good models by the parts. Such a function starts with a value at least zero for no partition of the data set and descents to zero for the partition of the data set into singleton parts. The optimal clustering is the one chosen to minimize the cluster structure function. The theory behind the method is expressed in algorithmic information theory (Kolmogorov complexity). In practice the Kolmogorov complexities involved are approximated by a concrete compressor. We give examples using real data sets: the MNIST handwritten digits and the segmentation of real cells as used in stem cell research.

Language learning from positive evidence, reconsidered: A simplicity-based approach

Children learn their native language by exposure to their linguistic and communicative environment, but apparently without requiring that their mistakes are corrected. Such learning from positive evidence has been viewed as raising logical problems for language acquisition. In particular, without correction, how is the child to recover from conjecturing an over-general grammar, which will be consistent with any sentence that the child hears? There have been many proposals concerning how this logical problem can be dissolved. Here, we review recent formal results showing that the learner has sufficient data to learn successfully from positive evidence, if it favours the simplest encoding of the linguistic input. Results include the ability to learn a linguistic prediction, grammaticality judgements, language production, and form-meaning mappings. The simplicity approach can also be scaled-down to analyse the ability to learn a specific linguistic constructions, and is amenable to empirical test as a framework for describing human language acquisition.

On Empirical Entropy

We propose a compression-based version of the empirical entropy of a finite string over a finite alphabet. Whereas previously one considers the naked entropy of (possibly higher order) Markov processes, we consider the sum of the description of the random variable involved plus the entropy it induces. We assume only that the distribution involved is computable. To test the new notion we compare the Normalized Information Distance (the similarity metric) with a related measure based on Mutual Information in Shannon's framework. This way the similarities and differences of the last two concepts are exposed.