Integral Probability Metrics PAC-Bayes Bounds

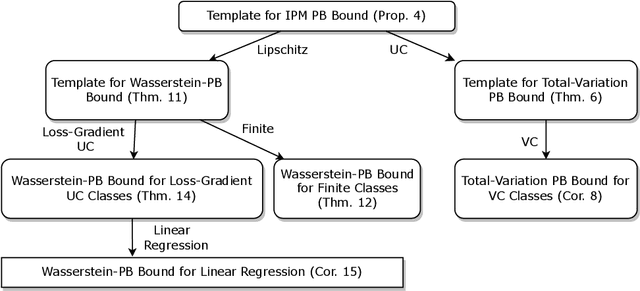
We present a PAC-Bayes-style generalization bound which enables the replacement of the KL-divergence with a variety of Integral Probability Metrics (IPM). We provide instances of this bound with the IPM being the total variation metric and the Wasserstein distance. A notable feature of the obtained bounds is that they naturally interpolate between classical uniform convergence bounds in the worst case (when the prior and posterior are far away from each other), and preferable bounds in better cases (when the posterior and prior are close). This illustrates the possibility of reinforcing classical generalization bounds with algorithm- and data-dependent components, thus making them more suitable to analyze algorithms that use a large hypothesis space.

Discount Factor as a Regularizer in Reinforcement Learning

Specifying a Reinforcement Learning (RL) task involves choosing a suitable planning horizon, which is typically modeled by a discount factor. It is known that applying RL algorithms with a lower discount factor can act as a regularizer, improving performance in the limited data regime. Yet the exact nature of this regularizer has not been investigated. In this work, we fill in this gap. For several Temporal-Difference (TD) learning methods, we show an explicit equivalence between using a reduced discount factor and adding an explicit regularization term to the algorithm's loss. Motivated by the equivalence, we empirically study this technique compared to standard $L_2$ regularization by extensive experiments in discrete and continuous domains, using tabular and functional representations. Our experiments suggest the regularization effectiveness is strongly related to properties of the available data, such as size, distribution, and mixing rate.

Meta-Learning by Adjusting Priors Based on Extended PAC-Bayes Theory

In meta-learning an agent extracts knowledge from observed tasks, aiming to facilitate learning of novel future tasks. Under the assumption that future tasks are 'related' to previous tasks, the accumulated knowledge should be learned in a way which captures the common structure across learned tasks, while allowing the learner sufficient flexibility to adapt to novel aspects of new tasks. We present a framework for meta-learning that is based on generalization error bounds, allowing us to extend various PAC-Bayes bounds to meta-learning. Learning takes place through the construction of a distribution over hypotheses based on the observed tasks, and its utilization for learning a new task. Thus, prior knowledge is incorporated through setting an experience-dependent prior for novel tasks. We develop a gradient-based algorithm which minimizes an objective function derived from the bounds and demonstrate its effectiveness numerically with deep neural networks. In addition to establishing the improved performance available through meta-learning, we demonstrate the intuitive way by which prior information is manifested at different levels of the network.