Integral Probability Metrics PAC-Bayes Bounds
Paper and Code
Jul 06, 2022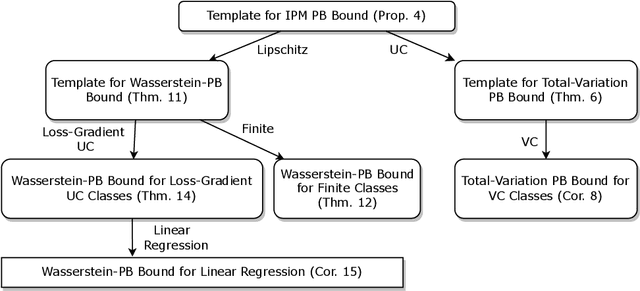
We present a PAC-Bayes-style generalization bound which enables the replacement of the KL-divergence with a variety of Integral Probability Metrics (IPM). We provide instances of this bound with the IPM being the total variation metric and the Wasserstein distance. A notable feature of the obtained bounds is that they naturally interpolate between classical uniform convergence bounds in the worst case (when the prior and posterior are far away from each other), and preferable bounds in better cases (when the posterior and prior are close). This illustrates the possibility of reinforcing classical generalization bounds with algorithm- and data-dependent components, thus making them more suitable to analyze algorithms that use a large hypothesis space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge