Markov Chain-based Optimization Time Analysis of Bivalent Ant Colony Optimization for Sorting and LeadingOnes

So far, only few bounds on the runtime behavior of Ant Colony Optimization (ACO) have been reported. To alleviate this situation, we investigate the ACO variant we call Bivalent ACO (BACO) that uses exactly two pheromone values. We provide and successfully apply a new Markov chain-based approach to calculate the expected optimization time, i. e., the expected number of iterations until the algorithm terminates. This approach allows to derive exact formulae for the expected optimization time for the problems Sorting and LeadingOnes. It turns out that the ratio of the two pheromone values significantly governs the runtime behavior of BACO. To the best of our knowledge, for the first time, we can present tight bounds for Sorting ($\Theta(n^3)$) with a specifically chosen objective function and prove the missing lower bound $\Omega(n^2)$ for LeadingOnes which, thus, is tightly bounded by $\Theta(n^2)$. We show that despite we have a drastically simplified ant algorithm with respect to the influence of the pheromones on the solving process, known bounds on the expected optimization time for the problems OneMax ($O(n\log n)$) and LeadingOnes ($O(n^2)$) can be re-produced as a by-product of our approach. Experiments validate our theoretical findings.

Robustness Approaches for the Examination Timetabling Problem under Data Uncertainty

In the literature the examination timetabling problem (ETTP) is often considered a post-enrollment problem (PE-ETTP). In the real world, universities often schedule their exams before students register using information from previous terms. A direct consequence of this approach is the uncertainty present in the resulting models. In this work we discuss several approaches available in the robust optimization literature. We consider the implications of each approach in respect to the examination timetabling problem and present how the most favorable approaches can be applied to the ETTP. Afterwards we analyze the impact of some possible implementations of the given robustness approaches on two real world instances and several random instances generated by our instance generation framework which we introduce in this work.

The Convergence Indicator: Improved and completely characterized parameter bounds for actual convergence of Particle Swarm Optimization

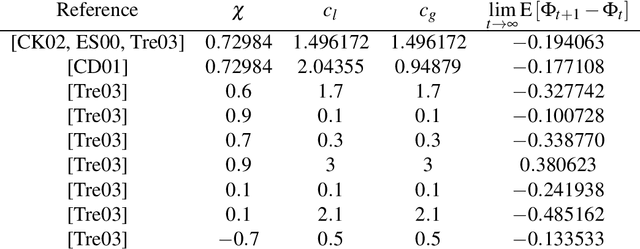
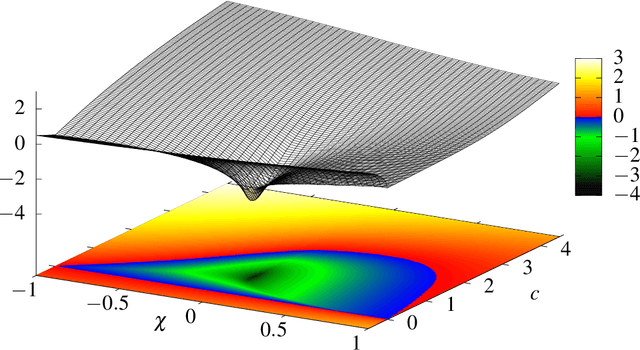
Particle Swarm Optimization (PSO) is a meta-heuristic for continuous black-box optimization problems. In this paper we focus on the convergence of the particle swarm, i.e., the exploitation phase of the algorithm. We introduce a new convergence indicator that can be used to calculate whether the particles will finally converge to a single point or diverge. Using this convergence indicator we provide the actual bounds completely characterizing parameter regions that lead to a converging swarm. Our bounds extend the parameter regions where convergence is guaranteed compared to bounds induced by converging variance which are usually used in the literature. To evaluate our criterion we describe a numerical approximation using cubic spline interpolation. Finally we provide experiments showing that our concept, formulas and the resulting convergence bounds represent the actual behavior of PSO.

Explanation of Stagnation at Points that are not Local Optima in Particle Swarm Optimization by Potential Analysis

Particle Swarm Optimization (PSO) is a nature-inspired meta-heuristic for solving continuous optimization problems. In the literature, the potential of the particles of swarm has been used to show that slightly modified PSO guarantees convergence to local optima. Here we show that under specific circumstances the unmodified PSO, even with swarm parameters known (from the literature) to be good, almost surely does not yield convergence to a local optimum is provided. This undesirable phenomenon is called stagnation. For this purpose, the particles' potential in each dimension is analyzed mathematically. Additionally, some reasonable assumptions on the behavior if the particles' potential are made. Depending on the objective function and, interestingly, the number of particles, the potential in some dimensions may decrease much faster than in other dimensions. Therefore, these dimensions lose relevance, i.e., the contribution of their entries to the decisions about attractor updates becomes insignificant and, with positive probability, they never regain relevance. If Brownian Motion is assumed to be an approximation of the time-dependent drop of potential, practical, i.e., large values for this probability are calculated. Finally, on chosen multidimensional polynomials of degree two, experiments are provided showing that the required circumstances occur quite frequently. Furthermore, experiments are provided showing that even when the very simple sphere function is processed the described stagnation phenomenon occurs. Consequently, unmodified PSO does not converge to any local optimum of the chosen functions for tested parameter settings.

Towards a Better Understanding of the Local Attractor in Particle Swarm Optimization: Speed and Solution Quality

Particle Swarm Optimization (PSO) is a popular nature-inspired meta-heuristic for solving continuous optimization problems. Although this technique is widely used, the understanding of the mechanisms that make swarms so successful is still limited. We present the first substantial experimental investigation of the influence of the local attractor on the quality of exploration and exploitation. We compare in detail classical PSO with the social-only variant where local attractors are ignored. To measure the exploration capabilities, we determine how frequently both variants return results in the neighborhood of the global optimum. We measure the quality of exploitation by considering only function values from runs that reached a search point sufficiently close to the global optimum and then comparing in how many digits such values still deviate from the global minimum value. It turns out that the local attractor significantly improves the exploration, but sometimes reduces the quality of the exploitation. As a compromise, we propose and evaluate a hybrid PSO which switches off its local attractors at a certain point in time. The effects mentioned can also be observed by measuring the potential of the swarm.

A Decomposition of the Max-min Fair Curriculum-based Course Timetabling Problem

We propose a decomposition of the max-min fair curriculum-based course timetabling (MMF-CB-CTT) problem. The decomposition models the room assignment subproblem as a generalized lexicographic bottleneck optimization problem (LBOP). We show that the generalized LBOP can be solved efficiently if the corresponding sum optimization problem can be solved efficiently. As a consequence, the room assignment subproblem of the MMF-CB-CTT problem can be solved efficiently. We use this insight to improve a previously proposed heuristic algorithm for the MMF-CB-CTT problem. Our experimental results indicate that using the new decomposition improves the performance of the algorithm on most of the 21 ITC2007 test instances with respect to the quality of the best solution found. Furthermore, we introduce a measure of the quality of a solution to a max-min fair optimization problem. This measure helps to overcome some limitations imposed by the qualitative nature of max-min fairness and aids the statistical evaluation of the performance of randomized algorithms for such problems. We use this measure to show that using the new decomposition the algorithm outperforms the original one on most instances with respect to the average solution quality.

Particles Prefer Walking Along the Axes: Experimental Insights into the Behavior of a Particle Swarm

Particle swarm optimization (PSO) is a widely used nature-inspired meta-heuristic for solving continuous optimization problems. However, when running the PSO algorithm, one encounters the phenomenon of so-called stagnation, that means in our context, the whole swarm starts to converge to a solution that is not (even a local) optimum. The goal of this work is to point out possible reasons why the swarm stagnates at these non-optimal points. To achieve our results, we use the newly defined potential of a swarm. The total potential has a portion for every dimension of the search space, and it drops when the swarm approaches the point of convergence. As it turns out experimentally, the swarm is very likely to come sometimes into "unbalanced" states, i. e., almost all potential belongs to one axis. Therefore, the swarm becomes blind for improvements still possible in any other direction. Finally, we show how in the light of the potential and these observations, a slightly adapted PSO rebalances the potential and therefore increases the quality of the solution.

Fairness in Academic Course Timetabling

We consider the problem of creating fair course timetables in the setting of a university. Our motivation is to improve the overall satisfaction of individuals concerned (students, teachers, etc.) by providing a fair timetable to them. The central idea is that undesirable arrangements in the course timetable, i.e., violations of soft constraints, should be distributed in a fair way among the individuals. We propose two formulations for the fair course timetabling problem that are based on max-min fairness and Jain's fairness index, respectively. Furthermore, we present and experimentally evaluate an optimization algorithm based on simulated annealing for solving max-min fair course timetabling problems. The new contribution is concerned with measuring the energy difference between two timetables, i.e., how much worse a timetable is compared to another timetable with respect to max-min fairness. We introduce three different energy difference measures and evaluate their impact on the overall algorithm performance. The second proposed problem formulation focuses on the tradeoff between fairness and the total amount of soft constraint violations. Our experimental evaluation shows that the known best solutions to the ITC2007 curriculum-based course timetabling instances are quite fair with respect to Jain's fairness index. However, the experiments also show that the fairness can be improved further for only a rather small increase in the total amount of soft constraint violations.