The Convergence Indicator: Improved and completely characterized parameter bounds for actual convergence of Particle Swarm Optimization
Paper and Code
Jun 06, 2020
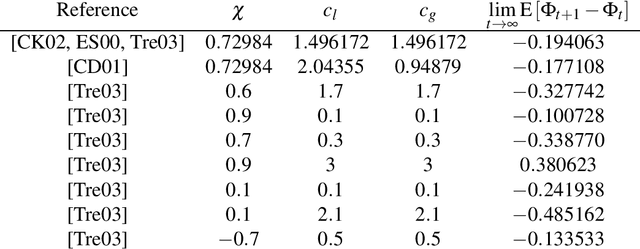
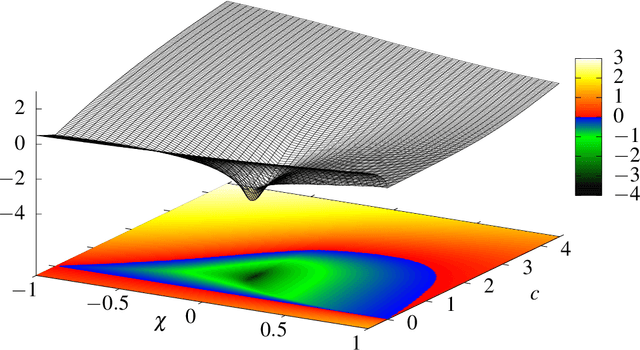

Particle Swarm Optimization (PSO) is a meta-heuristic for continuous black-box optimization problems. In this paper we focus on the convergence of the particle swarm, i.e., the exploitation phase of the algorithm. We introduce a new convergence indicator that can be used to calculate whether the particles will finally converge to a single point or diverge. Using this convergence indicator we provide the actual bounds completely characterizing parameter regions that lead to a converging swarm. Our bounds extend the parameter regions where convergence is guaranteed compared to bounds induced by converging variance which are usually used in the literature. To evaluate our criterion we describe a numerical approximation using cubic spline interpolation. Finally we provide experiments showing that our concept, formulas and the resulting convergence bounds represent the actual behavior of PSO.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge