Robustness Approaches for the Examination Timetabling Problem under Data Uncertainty

In the literature the examination timetabling problem (ETTP) is often considered a post-enrollment problem (PE-ETTP). In the real world, universities often schedule their exams before students register using information from previous terms. A direct consequence of this approach is the uncertainty present in the resulting models. In this work we discuss several approaches available in the robust optimization literature. We consider the implications of each approach in respect to the examination timetabling problem and present how the most favorable approaches can be applied to the ETTP. Afterwards we analyze the impact of some possible implementations of the given robustness approaches on two real world instances and several random instances generated by our instance generation framework which we introduce in this work.

The Convergence Indicator: Improved and completely characterized parameter bounds for actual convergence of Particle Swarm Optimization

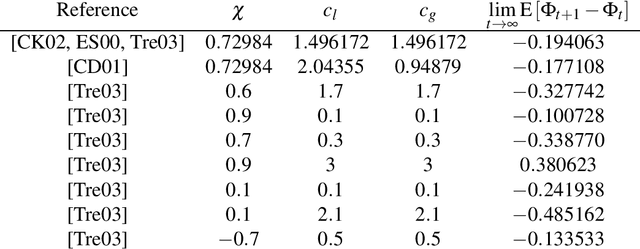
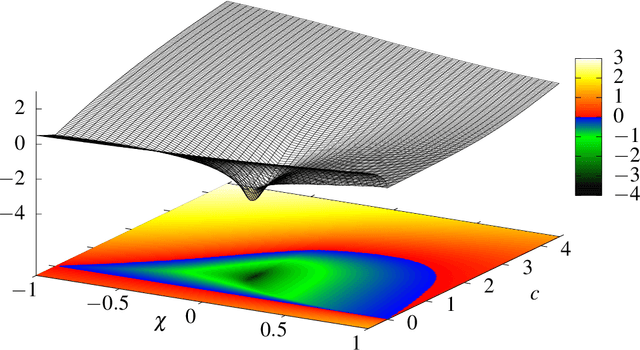
Particle Swarm Optimization (PSO) is a meta-heuristic for continuous black-box optimization problems. In this paper we focus on the convergence of the particle swarm, i.e., the exploitation phase of the algorithm. We introduce a new convergence indicator that can be used to calculate whether the particles will finally converge to a single point or diverge. Using this convergence indicator we provide the actual bounds completely characterizing parameter regions that lead to a converging swarm. Our bounds extend the parameter regions where convergence is guaranteed compared to bounds induced by converging variance which are usually used in the literature. To evaluate our criterion we describe a numerical approximation using cubic spline interpolation. Finally we provide experiments showing that our concept, formulas and the resulting convergence bounds represent the actual behavior of PSO.