Rohan Budhiraja
Crocoddyl: An Efficient and Versatile Framework for Multi-Contact Optimal Control
Sep 11, 2019



Abstract:We introduce Crocoddyl (Contact RObot COntrol by Differential DYnamic Library), an open-source framework tailored for efficient multi-contact optimal control. Crocoddyl efficiently computes the state trajectory and the control policy for a given predefined sequence of contacts. Its efficiency is due to the use of sparse analytical derivatives, exploitation of the problem structure, and data sharing. It employs differential geometry to properly describe the state of any geometrical system, e.g. floating-base systems. We have unified dynamics, costs, and constraints into a single concept -- action -- for greater efficiency and easy prototyping. Additionally, we propose a novel multiple-shooting method called Feasibility-prone Differential Dynamic Programming (FDDP). Our novel method shows a greater globalization strategy compared to classical Differential Dynamic Programming (DDP) algorithms, and it has similar numerical behavior to state-of-the-art multiple-shooting methods. However, our method does not increase the computational complexity typically encountered by adding extra variables to describe the gaps in the dynamics. Concretely, we propose two modifications to the classical DDP algorithm. First, the backward pass accepts infeasible state-control trajectories. Second, the rollout keeps the gaps open during the early "exploratory" iterations (as expected in multiple-shooting methods). We showcase the performance of our framework using different tasks. With our method, we can compute highly-dynamic maneuvers for legged robots (e.g. jumping, front-flip) in the order of milliseconds.
Differential Dynamic Programming for Multi-Phase Rigid Contact Dynamics
Apr 10, 2019
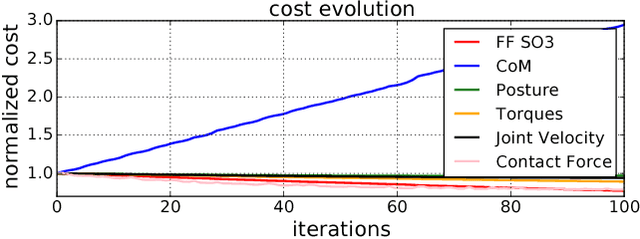
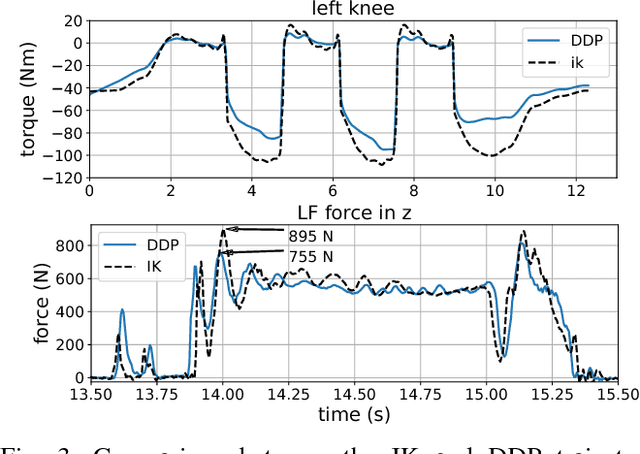
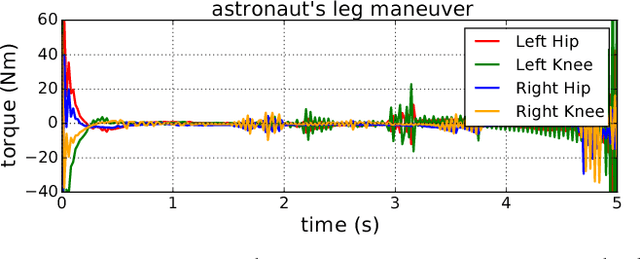
Abstract:A common strategy today to generate efficient locomotion movements is to split the problem into two consecutive steps: the first one generates the contact sequence together with the centroidal trajectory, while the second one computes the whole-body trajectory that follows the centroidal pattern. Yet the second step is generally handled by a simple program such as an inverse kinematics solver. In contrast, we propose to compute the whole-body trajectory by using a local optimal control solver, namely Differential Dynamic Programming (DDP). Our method produces more efficient motions, with lower forces and smaller impacts, by exploiting the Angular Momentum (AM). With this aim, we propose an original DDP formulation exploiting the Karush-Kuhn-Tucker constraint of the rigid contact model. We experimentally show the importance of this approach by executing large steps walking on the real HRP-2 robot, and by solving the problem of attitude control under the absence of external forces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge