Physical Symbolic Optimization

We present a framework for constraining the automatic sequential generation of equations to obey the rules of dimensional analysis by construction. Combining this approach with reinforcement learning, we built $\Phi$-SO, a Physical Symbolic Optimization method for recovering analytical functions from physical data leveraging units constraints. Our symbolic regression algorithm achieves state-of-the-art results in contexts in which variables and constants have known physical units, outperforming all other methods on SRBench's Feynman benchmark in the presence of noise (exceeding 0.1%) and showing resilience even in the presence of significant (10%) levels of noise.

Class Symbolic Regression: Gotta Fit 'Em All

We introduce "Class Symbolic Regression" a first framework for automatically finding a single analytical functional form that accurately fits multiple datasets - each governed by its own (possibly) unique set of fitting parameters. This hierarchical framework leverages the common constraint that all the members of a single class of physical phenomena follow a common governing law. Our approach extends the capabilities of our earlier Physical Symbolic Optimization ($\Phi$-SO) framework for Symbolic Regression, which integrates dimensional analysis constraints and deep reinforcement learning for symbolic analytical function discovery from data. We demonstrate the efficacy of this novel approach by applying it to a panel of synthetic toy case datasets and showcase its practical utility for astrophysics by successfully extracting an analytic galaxy potential from a set of simulated orbits approximating stellar streams.

SSG2: A new modelling paradigm for semantic segmentation

State-of-the-art models in semantic segmentation primarily operate on single, static images, generating corresponding segmentation masks. This one-shot approach leaves little room for error correction, as the models lack the capability to integrate multiple observations for enhanced accuracy. Inspired by work on semantic change detection, we address this limitation by introducing a methodology that leverages a sequence of observables generated for each static input image. By adding this "temporal" dimension, we exploit strong signal correlations between successive observations in the sequence to reduce error rates. Our framework, dubbed SSG2 (Semantic Segmentation Generation 2), employs a dual-encoder, single-decoder base network augmented with a sequence model. The base model learns to predict the set intersection, union, and difference of labels from dual-input images. Given a fixed target input image and a set of support images, the sequence model builds the predicted mask of the target by synthesizing the partial views from each sequence step and filtering out noise. We evaluate SSG2 across three diverse datasets: UrbanMonitor, featuring orthoimage tiles from Darwin, Australia with five spectral bands and 0.2m spatial resolution; ISPRS Potsdam, which includes true orthophoto images with multiple spectral bands and a 5cm ground sampling distance; and ISIC2018, a medical dataset focused on skin lesion segmentation, particularly melanoma. The SSG2 model demonstrates rapid convergence within the first few tens of epochs and significantly outperforms UNet-like baseline models with the same number of gradient updates. However, the addition of the temporal dimension results in an increased memory footprint. While this could be a limitation, it is offset by the advent of higher-memory GPUs and coding optimizations.

An end-to-end strategy for recovering a free-form potential from a snapshot of stellar coordinates

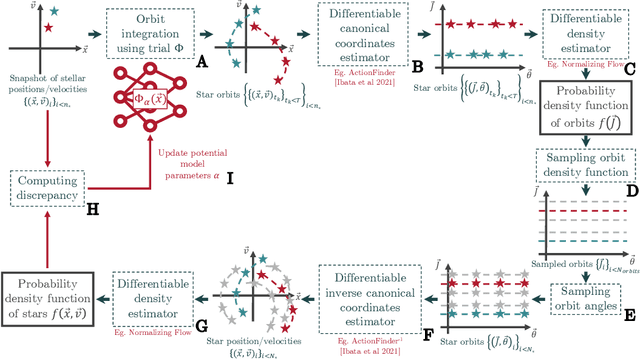
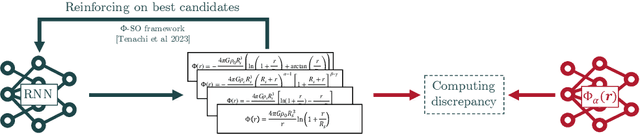
New large observational surveys such as Gaia are leading us into an era of data abundance, offering unprecedented opportunities to discover new physical laws through the power of machine learning. Here we present an end-to-end strategy for recovering a free-form analytical potential from a mere snapshot of stellar positions and velocities. First we show how auto-differentiation can be used to capture an agnostic map of the gravitational potential and its underlying dark matter distribution in the form of a neural network. However, in the context of physics, neural networks are both a plague and a blessing as they are extremely flexible for modeling physical systems but largely consist in non-interpretable black boxes. Therefore, in addition, we show how a complementary symbolic regression approach can be used to open up this neural network into a physically meaningful expression. We demonstrate our strategy by recovering the potential of a toy isochrone system.

Deep symbolic regression for physics guided by units constraints: toward the automated discovery of physical laws

Symbolic Regression is the study of algorithms that automate the search for analytic expressions that fit data. While recent advances in deep learning have generated renewed interest in such approaches, efforts have not been focused on physics, where we have important additional constraints due to the units associated with our data. Here we present $\Phi$-SO, a Physical Symbolic Optimization framework for recovering analytical symbolic expressions from physics data using deep reinforcement learning techniques by learning units constraints. Our system is built, from the ground up, to propose solutions where the physical units are consistent by construction. This is useful not only in eliminating physically impossible solutions, but because it restricts enormously the freedom of the equation generator, thus vastly improving performance. The algorithm can be used to fit noiseless data, which can be useful for instance when attempting to derive an analytical property of a physical model, and it can also be used to obtain analytical approximations to noisy data. We showcase our machinery on a panel of examples from astrophysics.