Generalizing the SINDy approach with nested neural networks

Symbolic Regression (SR) is a widely studied field of research that aims to infer symbolic expressions from data. A popular approach for SR is the Sparse Identification of Nonlinear Dynamical Systems (\sindy) framework, which uses sparse regression to identify governing equations from data. This study introduces an enhanced method, Nested SINDy, that aims to increase the expressivity of the SINDy approach thanks to a nested structure. Indeed, traditional symbolic regression and system identification methods often fail with complex systems that cannot be easily described analytically. Nested SINDy builds on the SINDy framework by introducing additional layers before and after the core SINDy layer. This allows the method to identify symbolic representations for a wider range of systems, including those with compositions and products of functions. We demonstrate the ability of the Nested SINDy approach to accurately find symbolic expressions for simple systems, such as basic trigonometric functions, and sparse (false but accurate) analytical representations for more complex systems. Our results highlight Nested SINDy's potential as a tool for symbolic regression, surpassing the traditional SINDy approach in terms of expressivity. However, we also note the challenges in the optimization process for Nested SINDy and suggest future research directions, including the designing of a more robust methodology for the optimization process. This study proves that Nested SINDy can effectively discover symbolic representations of dynamical systems from data, offering new opportunities for understanding complex systems through data-driven methods.

Physical Symbolic Optimization

We present a framework for constraining the automatic sequential generation of equations to obey the rules of dimensional analysis by construction. Combining this approach with reinforcement learning, we built $\Phi$-SO, a Physical Symbolic Optimization method for recovering analytical functions from physical data leveraging units constraints. Our symbolic regression algorithm achieves state-of-the-art results in contexts in which variables and constants have known physical units, outperforming all other methods on SRBench's Feynman benchmark in the presence of noise (exceeding 0.1%) and showing resilience even in the presence of significant (10%) levels of noise.

Class Symbolic Regression: Gotta Fit 'Em All

We introduce "Class Symbolic Regression" a first framework for automatically finding a single analytical functional form that accurately fits multiple datasets - each governed by its own (possibly) unique set of fitting parameters. This hierarchical framework leverages the common constraint that all the members of a single class of physical phenomena follow a common governing law. Our approach extends the capabilities of our earlier Physical Symbolic Optimization ($\Phi$-SO) framework for Symbolic Regression, which integrates dimensional analysis constraints and deep reinforcement learning for symbolic analytical function discovery from data. We demonstrate the efficacy of this novel approach by applying it to a panel of synthetic toy case datasets and showcase its practical utility for astrophysics by successfully extracting an analytic galaxy potential from a set of simulated orbits approximating stellar streams.

An end-to-end strategy for recovering a free-form potential from a snapshot of stellar coordinates

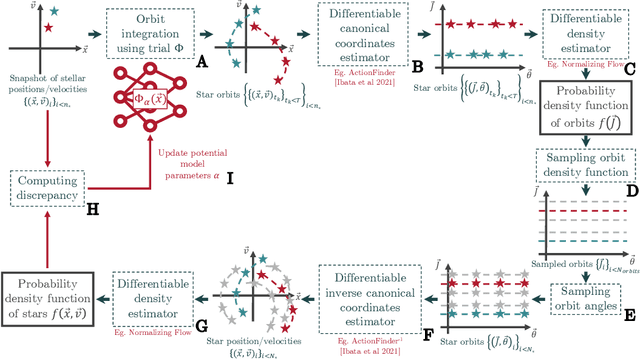
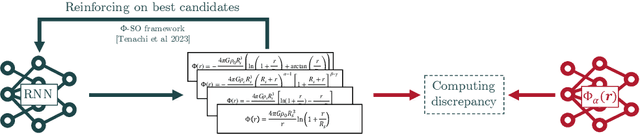
New large observational surveys such as Gaia are leading us into an era of data abundance, offering unprecedented opportunities to discover new physical laws through the power of machine learning. Here we present an end-to-end strategy for recovering a free-form analytical potential from a mere snapshot of stellar positions and velocities. First we show how auto-differentiation can be used to capture an agnostic map of the gravitational potential and its underlying dark matter distribution in the form of a neural network. However, in the context of physics, neural networks are both a plague and a blessing as they are extremely flexible for modeling physical systems but largely consist in non-interpretable black boxes. Therefore, in addition, we show how a complementary symbolic regression approach can be used to open up this neural network into a physically meaningful expression. We demonstrate our strategy by recovering the potential of a toy isochrone system.

Deep symbolic regression for physics guided by units constraints: toward the automated discovery of physical laws

Symbolic Regression is the study of algorithms that automate the search for analytic expressions that fit data. While recent advances in deep learning have generated renewed interest in such approaches, efforts have not been focused on physics, where we have important additional constraints due to the units associated with our data. Here we present $\Phi$-SO, a Physical Symbolic Optimization framework for recovering analytical symbolic expressions from physics data using deep reinforcement learning techniques by learning units constraints. Our system is built, from the ground up, to propose solutions where the physical units are consistent by construction. This is useful not only in eliminating physically impossible solutions, but because it restricts enormously the freedom of the equation generator, thus vastly improving performance. The algorithm can be used to fit noiseless data, which can be useful for instance when attempting to derive an analytical property of a physical model, and it can also be used to obtain analytical approximations to noisy data. We showcase our machinery on a panel of examples from astrophysics.