Coarse-Refinement Dilemma: On Generalization Bounds for Data Clustering

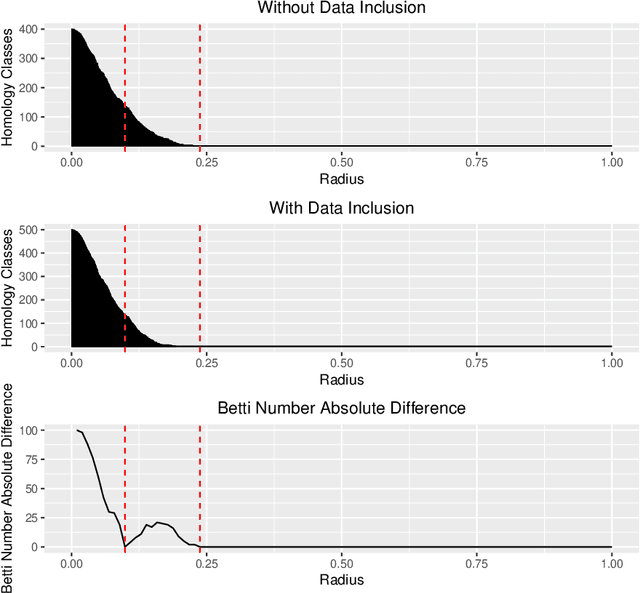
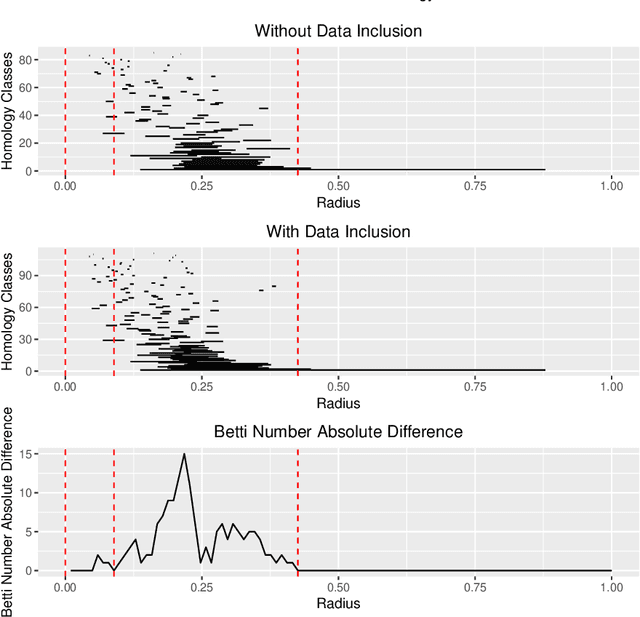
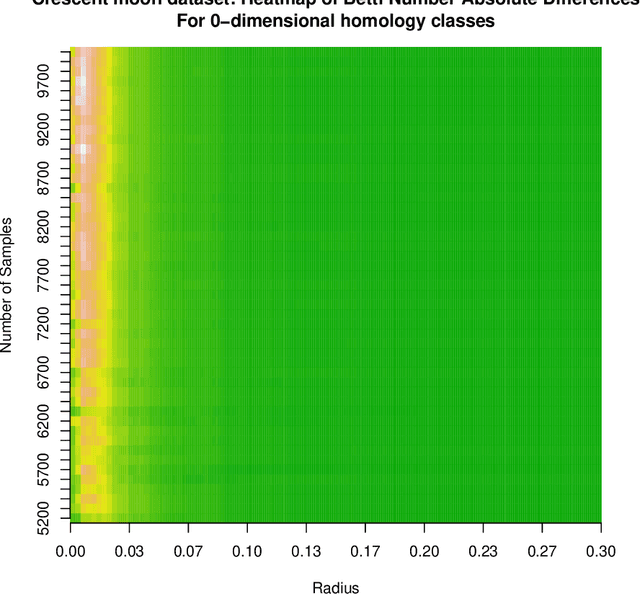
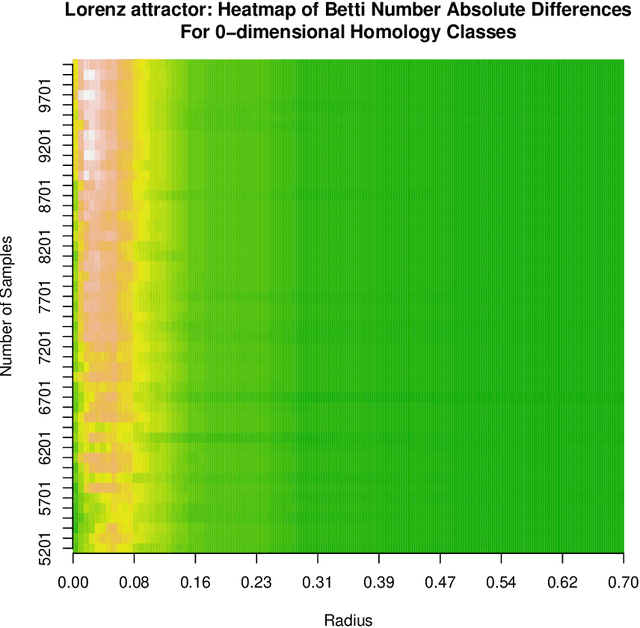
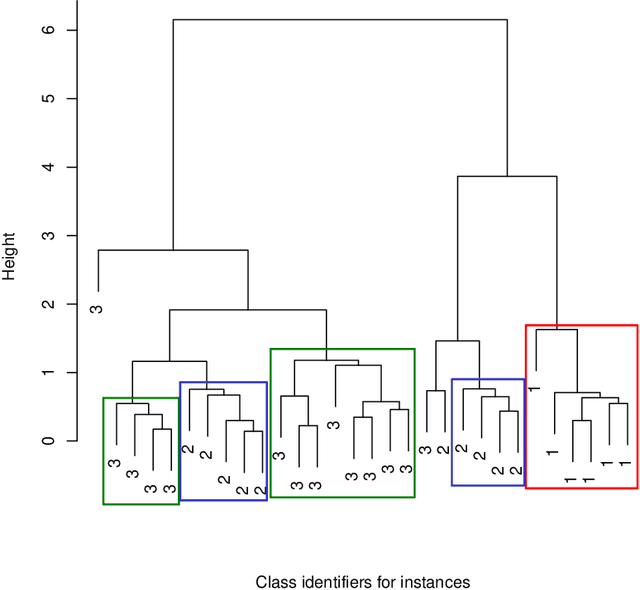
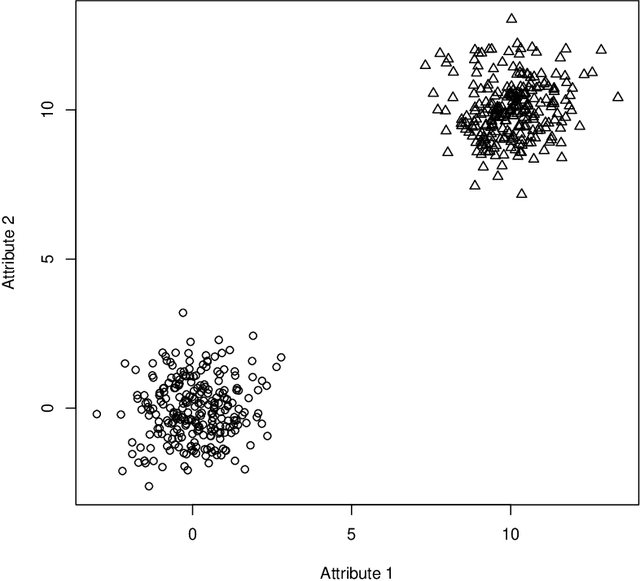
The Data Clustering (DC) problem is of central importance for the area of Machine Learning (ML), given its usefulness to represent data structural similarities from input spaces. Differently from Supervised Machine Learning (SML), which relies on the theoretical frameworks of the Statistical Learning Theory (SLT) and the Algorithm Stability (AS), DC has scarce literature on general-purpose learning guarantees, affecting conclusive remarks on how those algorithms should be designed as well as on the validity of their results. In this context, this manuscript introduces a new concept, based on multidimensional persistent homology, to analyze the conditions on which a clustering model is capable of generalizing data. As a first step, we propose a more general definition of DC problem by relying on Topological Spaces, instead of metric ones as typically approached in the literature. From that, we show that the DC problem presents an analogous dilemma to the Bias-Variance one, which is here referred to as the Coarse-Refinement (CR) dilemma. CR is intended to clarify the contrast between: (i) highly-refined partitions and the clustering instability (overfitting); and (ii) over-coarse partitions and the lack of representativeness (underfitting); consequently, the CR dilemma suggests the need of a relaxation of Kleinberg's richness axiom. Experimental results were used to illustrate that multidimensional persistent homology support the measurement of divergences among DC models, leading to a consistency criterion.

On the Shattering Coefficient of Supervised Learning Algorithms

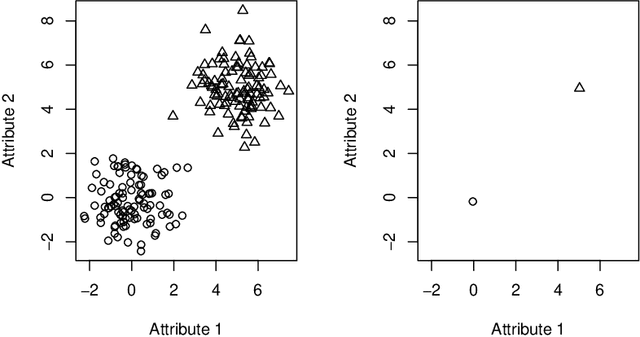
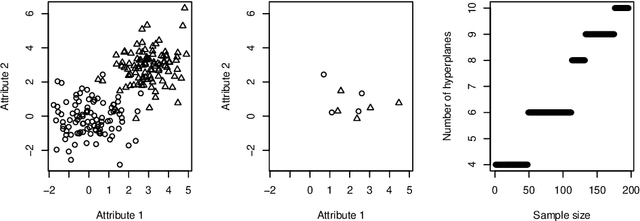
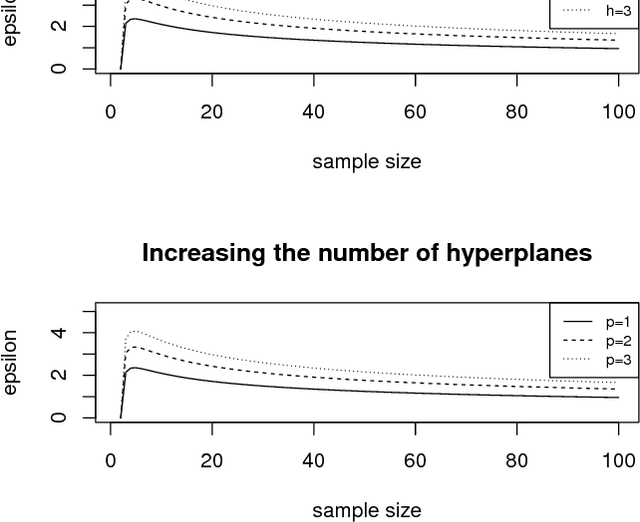
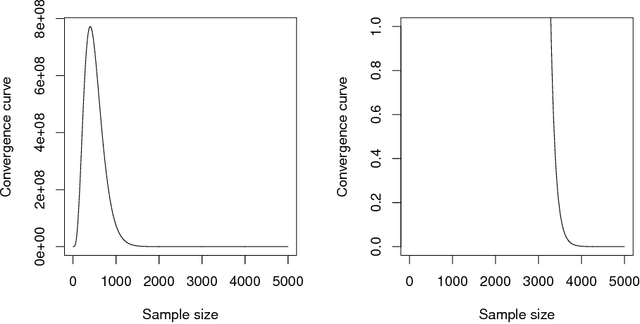
The Statistical Learning Theory (SLT) provides the theoretical background to ensure that a supervised algorithm generalizes the mapping $f: \mathcal{X} \to \mathcal{Y}$ given $f$ is selected from its search space bias $\mathcal{F}$. This formal result depends on the Shattering coefficient function $\mathcal{N}(\mathcal{F},2n)$ to upper bound the empirical risk minimization principle, from which one can estimate the necessary training sample size to ensure the probabilistic learning convergence and, most importantly, the characterization of the capacity of $\mathcal{F}$, including its under and overfitting abilities while addressing specific target problems. In this context, we propose a new approach to estimate the maximal number of hyperplanes required to shatter a given sample, i.e., to separate every pair of points from one another, based on the recent contributions by Har-Peled and Jones in the dataset partitioning scenario, and use such foundation to analytically compute the Shattering coefficient function for both binary and multi-class problems. As main contributions, one can use our approach to study the complexity of the search space bias $\mathcal{F}$, estimate training sample sizes, and parametrize the number of hyperplanes a learning algorithm needs to address some supervised task, what is specially appealing to deep neural networks. Experiments were performed to illustrate the advantages of our approach while studying the search space $\mathcal{F}$ on synthetic and one toy datasets and on two widely-used deep learning benchmarks (MNIST and CIFAR-10). In order to permit reproducibility and the use of our approach, our source code is made available at~\url{https://bitbucket.org/rodrigo_mello/shattering-rcode}.

Computing the Shattering Coefficient of Supervised Learning Algorithms

The Statistical Learning Theory (SLT) provides the theoretical guarantees for supervised machine learning based on the Empirical Risk Minimization Principle (ERMP). Such principle defines an upper bound to ensure the uniform convergence of the empirical risk Remp(f), i.e., the error measured on a given data sample, to the expected value of risk R(f) (a.k.a. actual risk), which depends on the Joint Probability Distribution P(X x Y) mapping input examples x in X to class labels y in Y. The uniform convergence is only ensured when the Shattering coefficient N(F,2n) has a polynomial growing behavior. This paper proves the Shattering coefficient for any Hilbert space H containing the input space X and discusses its effects in terms of learning guarantees for supervised machine algorithms.

Providing theoretical learning guarantees to Deep Learning Networks

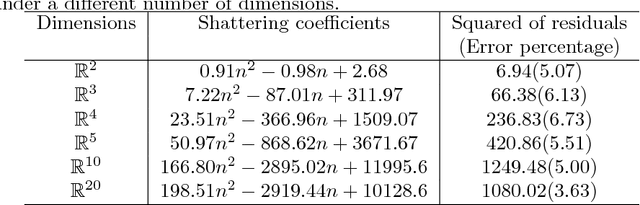
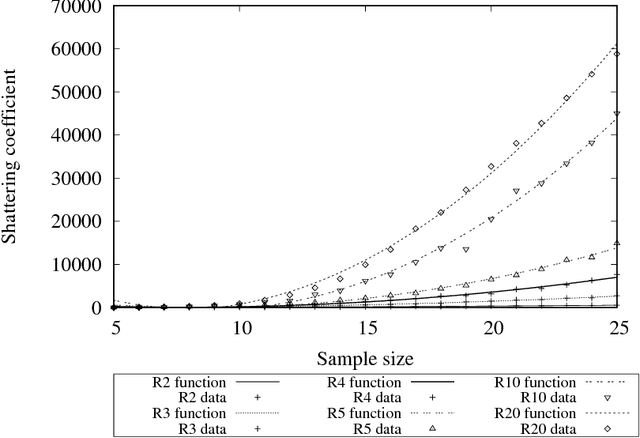
Deep Learning (DL) is one of the most common subjects when Machine Learning and Data Science approaches are considered. There are clearly two movements related to DL: the first aggregates researchers in quest to outperform other algorithms from literature, trying to win contests by considering often small decreases in the empirical risk; and the second investigates overfitting evidences, questioning the learning capabilities of DL classifiers. Motivated by such opposed points of view, this paper employs the Statistical Learning Theory (SLT) to study the convergence of Deep Neural Networks, with particular interest in Convolutional Neural Networks. In order to draw theoretical conclusions, we propose an approach to estimate the Shattering coefficient of those classification algorithms, providing a lower bound for the complexity of their space of admissible functions, a.k.a. algorithm bias. Based on such estimator, we generalize the complexity of network biases, and, next, we study AlexNet and VGG16 architectures in the point of view of their Shattering coefficients, and number of training examples required to provide theoretical learning guarantees. From our theoretical formulation, we show the conditions which Deep Neural Networks learn as well as point out another issue: DL benchmarks may be strictly driven by empirical risks, disregarding the complexity of algorithms biases.