On the Shattering Coefficient of Supervised Learning Algorithms

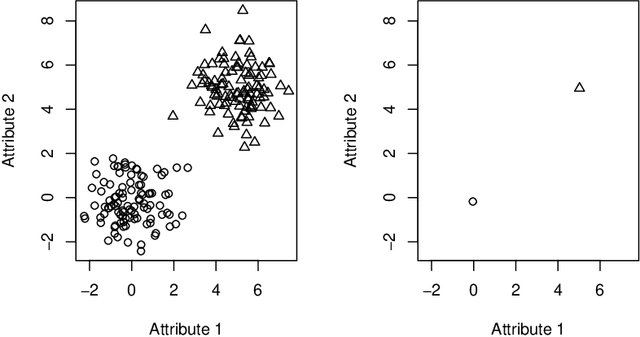
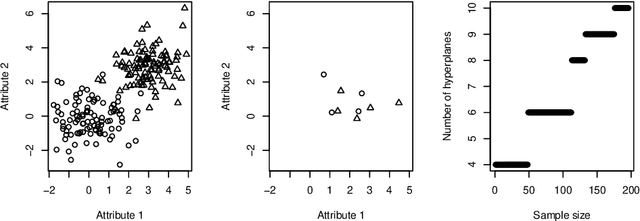
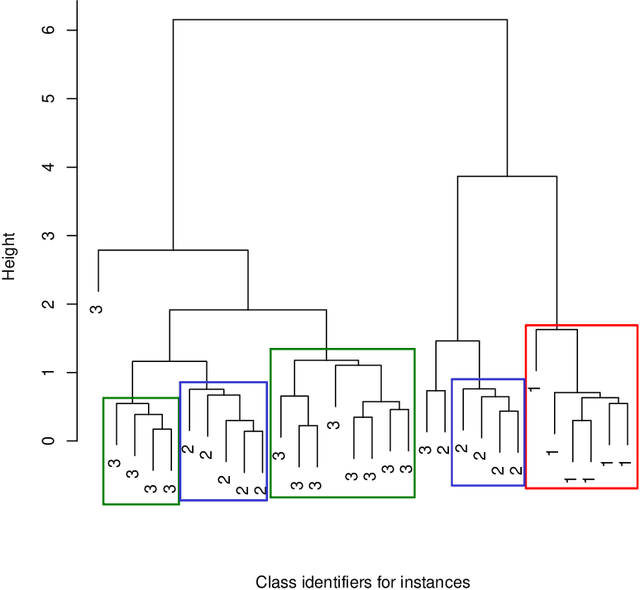
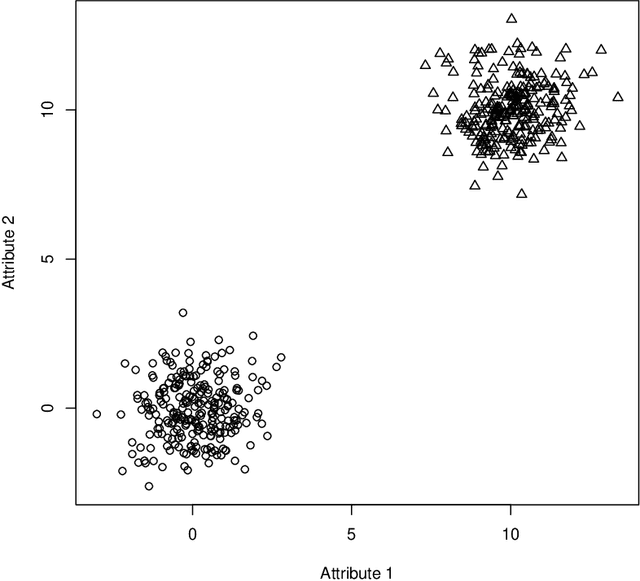
The Statistical Learning Theory (SLT) provides the theoretical background to ensure that a supervised algorithm generalizes the mapping $f: \mathcal{X} \to \mathcal{Y}$ given $f$ is selected from its search space bias $\mathcal{F}$. This formal result depends on the Shattering coefficient function $\mathcal{N}(\mathcal{F},2n)$ to upper bound the empirical risk minimization principle, from which one can estimate the necessary training sample size to ensure the probabilistic learning convergence and, most importantly, the characterization of the capacity of $\mathcal{F}$, including its under and overfitting abilities while addressing specific target problems. In this context, we propose a new approach to estimate the maximal number of hyperplanes required to shatter a given sample, i.e., to separate every pair of points from one another, based on the recent contributions by Har-Peled and Jones in the dataset partitioning scenario, and use such foundation to analytically compute the Shattering coefficient function for both binary and multi-class problems. As main contributions, one can use our approach to study the complexity of the search space bias $\mathcal{F}$, estimate training sample sizes, and parametrize the number of hyperplanes a learning algorithm needs to address some supervised task, what is specially appealing to deep neural networks. Experiments were performed to illustrate the advantages of our approach while studying the search space $\mathcal{F}$ on synthetic and one toy datasets and on two widely-used deep learning benchmarks (MNIST and CIFAR-10). In order to permit reproducibility and the use of our approach, our source code is made available at~\url{https://bitbucket.org/rodrigo_mello/shattering-rcode}.