Coarse-Refinement Dilemma: On Generalization Bounds for Data Clustering
Paper and Code
Nov 13, 2019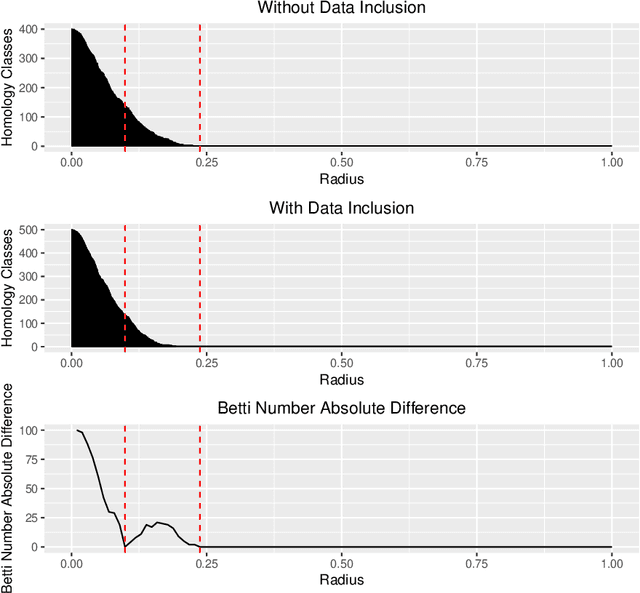
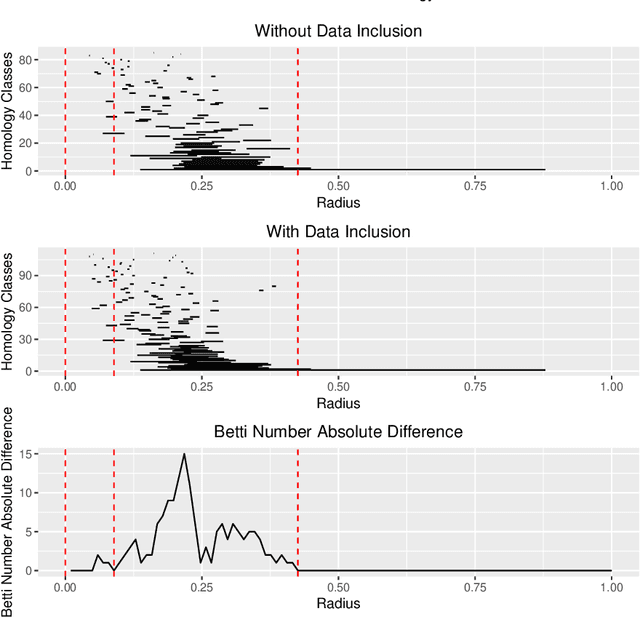
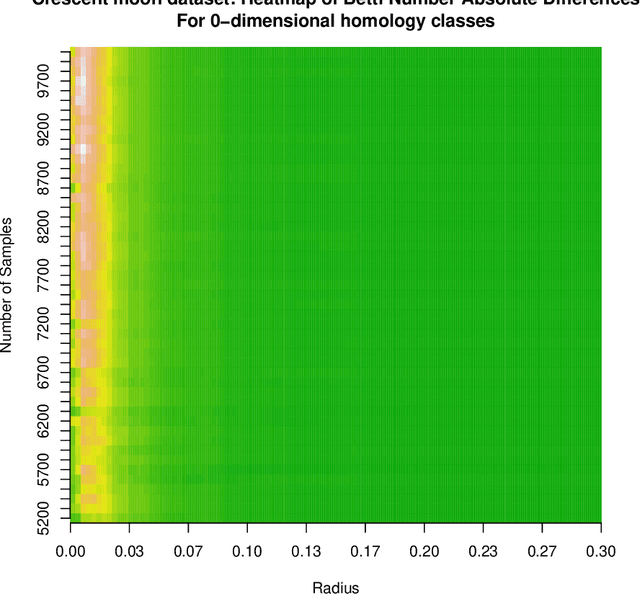
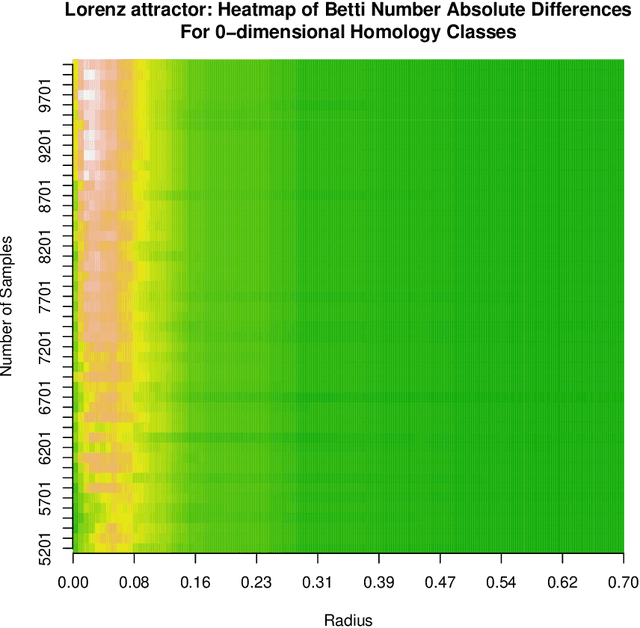
The Data Clustering (DC) problem is of central importance for the area of Machine Learning (ML), given its usefulness to represent data structural similarities from input spaces. Differently from Supervised Machine Learning (SML), which relies on the theoretical frameworks of the Statistical Learning Theory (SLT) and the Algorithm Stability (AS), DC has scarce literature on general-purpose learning guarantees, affecting conclusive remarks on how those algorithms should be designed as well as on the validity of their results. In this context, this manuscript introduces a new concept, based on multidimensional persistent homology, to analyze the conditions on which a clustering model is capable of generalizing data. As a first step, we propose a more general definition of DC problem by relying on Topological Spaces, instead of metric ones as typically approached in the literature. From that, we show that the DC problem presents an analogous dilemma to the Bias-Variance one, which is here referred to as the Coarse-Refinement (CR) dilemma. CR is intended to clarify the contrast between: (i) highly-refined partitions and the clustering instability (overfitting); and (ii) over-coarse partitions and the lack of representativeness (underfitting); consequently, the CR dilemma suggests the need of a relaxation of Kleinberg's richness axiom. Experimental results were used to illustrate that multidimensional persistent homology support the measurement of divergences among DC models, leading to a consistency criterion.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge