Providing theoretical learning guarantees to Deep Learning Networks
Paper and Code
Nov 28, 2017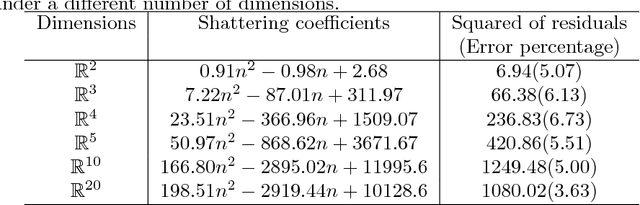
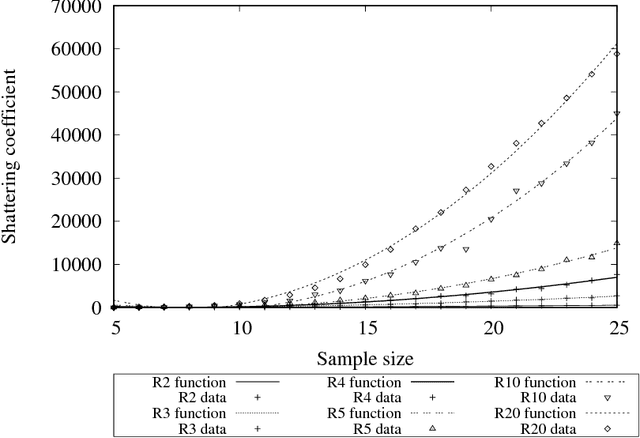
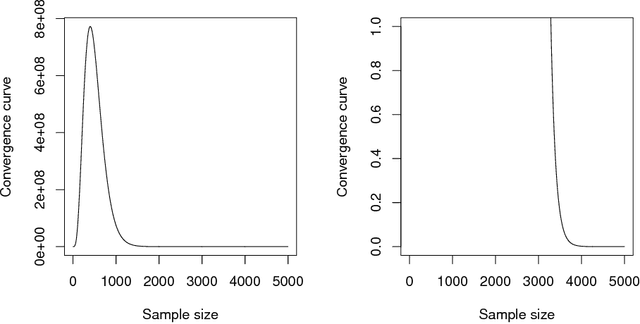

Deep Learning (DL) is one of the most common subjects when Machine Learning and Data Science approaches are considered. There are clearly two movements related to DL: the first aggregates researchers in quest to outperform other algorithms from literature, trying to win contests by considering often small decreases in the empirical risk; and the second investigates overfitting evidences, questioning the learning capabilities of DL classifiers. Motivated by such opposed points of view, this paper employs the Statistical Learning Theory (SLT) to study the convergence of Deep Neural Networks, with particular interest in Convolutional Neural Networks. In order to draw theoretical conclusions, we propose an approach to estimate the Shattering coefficient of those classification algorithms, providing a lower bound for the complexity of their space of admissible functions, a.k.a. algorithm bias. Based on such estimator, we generalize the complexity of network biases, and, next, we study AlexNet and VGG16 architectures in the point of view of their Shattering coefficients, and number of training examples required to provide theoretical learning guarantees. From our theoretical formulation, we show the conditions which Deep Neural Networks learn as well as point out another issue: DL benchmarks may be strictly driven by empirical risks, disregarding the complexity of algorithms biases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge