Unsupervised Learning of Group Invariant and Equivariant Representations

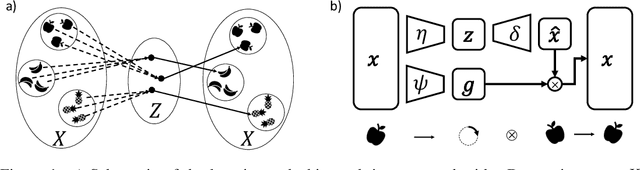
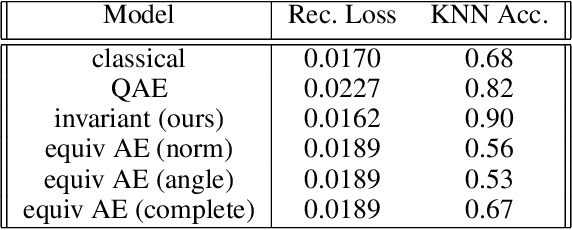
Equivariant neural networks, whose hidden features transform according to representations of a group G acting on the data, exhibit training efficiency and an improved generalisation performance. In this work, we extend group invariant and equivariant representation learning to the field of unsupervised deep learning. We propose a general learning strategy based on an encoder-decoder framework in which the latent representation is disentangled in an invariant term and an equivariant group action component. The key idea is that the network learns the group action on the data space and thus is able to solve the reconstruction task from an invariant data representation, hence avoiding the necessity of ad-hoc group-specific implementations. We derive the necessary conditions on the equivariant encoder, and we present a construction valid for any G, both discrete and continuous. We describe explicitly our construction for rotations, translations and permutations. We test the validity and the robustness of our approach in a variety of experiments with diverse data types employing different network architectures.

Permutation-Invariant Variational Autoencoder for Graph-Level Representation Learning

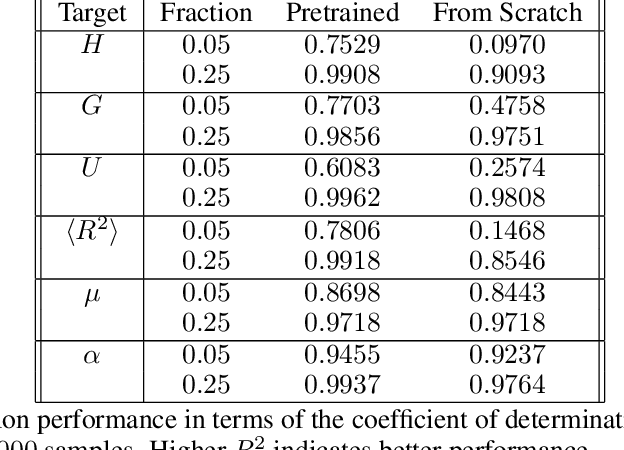
Recently, there has been great success in applying deep neural networks on graph structured data. Most work, however, focuses on either node- or graph-level supervised learning, such as node, link or graph classification or node-level unsupervised learning (e.g. node clustering). Despite its wide range of possible applications, graph-level unsupervised learning has not received much attention yet. This might be mainly attributed to the high representation complexity of graphs, which can be represented by n! equivalent adjacency matrices, where n is the number of nodes. In this work we address this issue by proposing a permutation-invariant variational autoencoder for graph structured data. Our proposed model indirectly learns to match the node ordering of input and output graph, without imposing a particular node ordering or performing expensive graph matching. We demonstrate the effectiveness of our proposed model on various graph reconstruction and generation tasks and evaluate the expressive power of extracted representations for downstream graph-level classification and regression.

Auto-Encoding Molecular Conformations

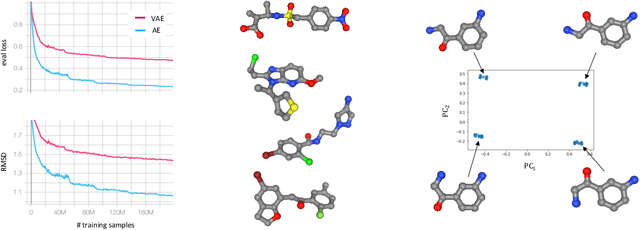
In this work we introduce an Autoencoder for molecular conformations. Our proposed model converts the discrete spatial arrangements of atoms in a given molecular graph (conformation) into and from a continuous fixed-sized latent representation. We demonstrate that in this latent representation, similar conformations cluster together while distinct conformations split apart. Moreover, by training a probabilistic model on a large dataset of molecular conformations, we demonstrate how our model can be used to generate diverse sets of energetically favorable conformations for a given molecule. Finally, we show that the continuous representation allows us to utilize optimization methods to find molecules that have conformations with favourable spatial properties.

IVE-GAN: Invariant Encoding Generative Adversarial Networks

Generative adversarial networks (GANs) are a powerful framework for generative tasks. However, they are difficult to train and tend to miss modes of the true data generation process. Although GANs can learn a rich representation of the covered modes of the data in their latent space, the framework misses an inverse mapping from data to this latent space. We propose Invariant Encoding Generative Adversarial Networks (IVE-GANs), a novel GAN framework that introduces such a mapping for individual samples from the data by utilizing features in the data which are invariant to certain transformations. Since the model maps individual samples to the latent space, it naturally encourages the generator to cover all modes. We demonstrate the effectiveness of our approach in terms of generative performance and learning rich representations on several datasets including common benchmark image generation tasks.