Unsupervised Learning of Group Invariant and Equivariant Representations

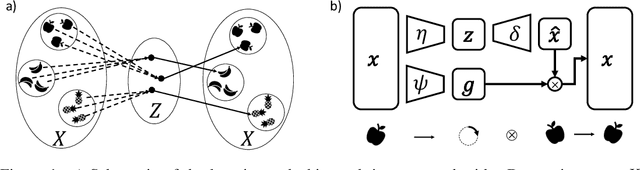
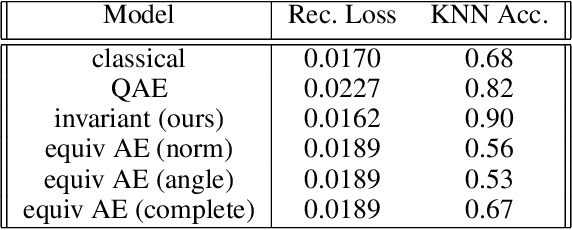
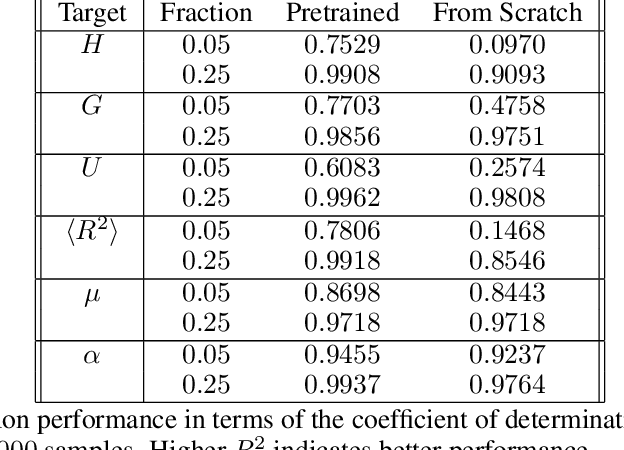
Equivariant neural networks, whose hidden features transform according to representations of a group G acting on the data, exhibit training efficiency and an improved generalisation performance. In this work, we extend group invariant and equivariant representation learning to the field of unsupervised deep learning. We propose a general learning strategy based on an encoder-decoder framework in which the latent representation is disentangled in an invariant term and an equivariant group action component. The key idea is that the network learns the group action on the data space and thus is able to solve the reconstruction task from an invariant data representation, hence avoiding the necessity of ad-hoc group-specific implementations. We derive the necessary conditions on the equivariant encoder, and we present a construction valid for any G, both discrete and continuous. We describe explicitly our construction for rotations, translations and permutations. We test the validity and the robustness of our approach in a variety of experiments with diverse data types employing different network architectures.