Parallel Algorithms for Exact Enumeration of Deep Neural Network Activation Regions

A feedforward neural network using rectified linear units constructs a mapping from inputs to outputs by partitioning its input space into a set of convex regions where points within a region share a single affine transformation. In order to understand how neural networks work, when and why they fail, and how they compare to biological intelligence, we need to understand the organization and formation of these regions. Step one is to design and implement algorithms for exact region enumeration in networks beyond toy examples. In this work, we present parallel algorithms for exact enumeration in deep (and shallow) neural networks. Our work has three main contributions: (1) we present a novel algorithm framework and parallel algorithms for region enumeration; (2) we implement one of our algorithms on a variety of network architectures and experimentally show how the number of regions dictates runtime; and (3) we show, using our algorithm's output, how the dimension of a region's affine transformation impacts further partitioning of the region by deeper layers. To our knowledge, we run our implemented algorithm on networks larger than all of the networks used in the existing region enumeration literature. Further, we experimentally demonstrate the importance of parallelism for region enumeration of any reasonably sized network.

Syntax-semantics interface: an algebraic model

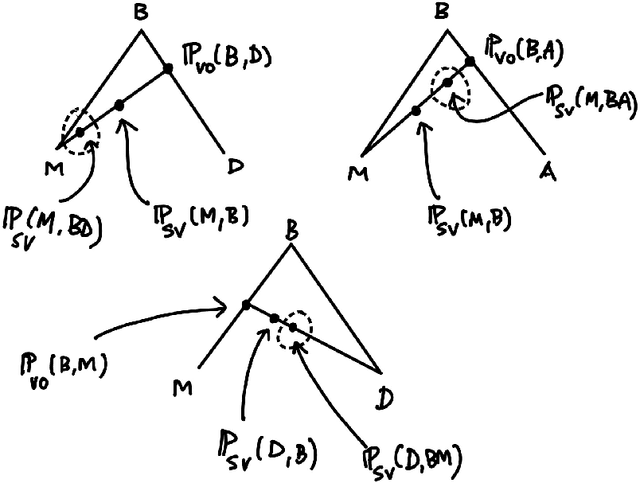
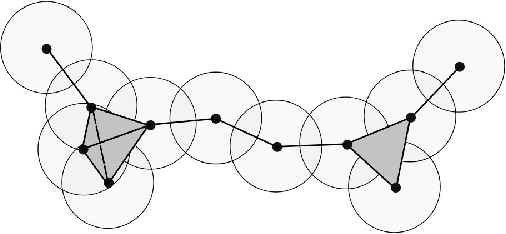
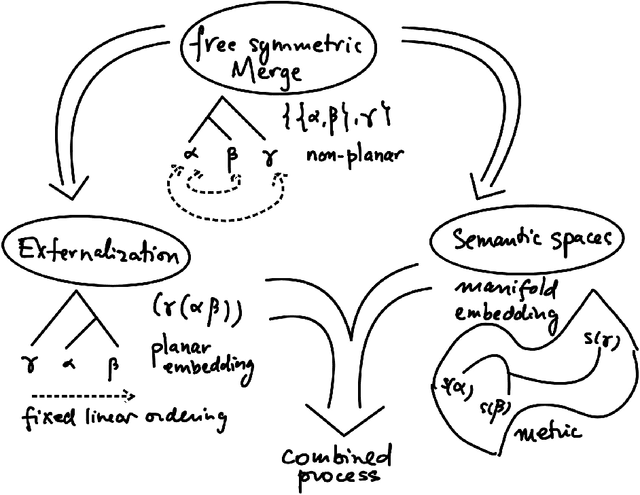
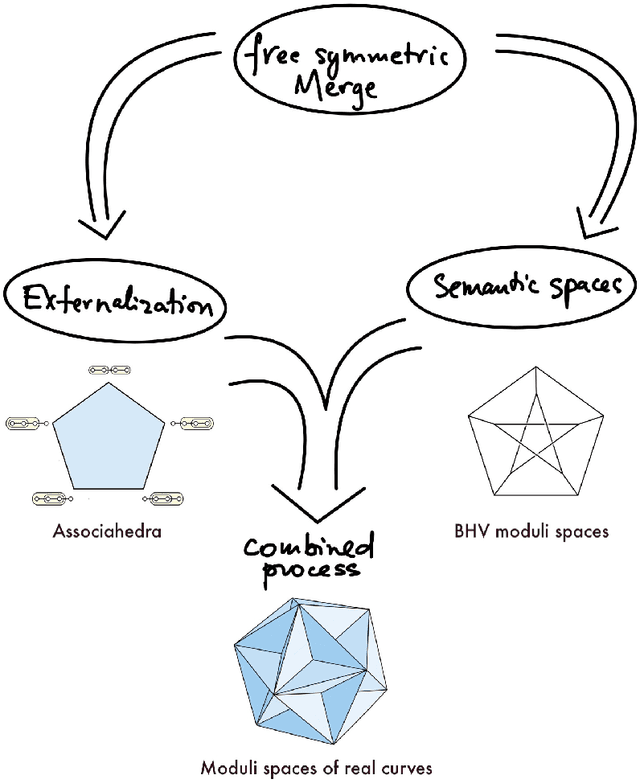
We extend our formulation of Merge and Minimalism in terms of Hopf algebras to an algebraic model of a syntactic-semantic interface. We show that methods adopted in the formulation of renormalization (extraction of meaningful physical values) in theoretical physics are relevant to describe the extraction of meaning from syntactic expressions. We show how this formulation relates to computational models of semantics and we answer some recent controversies about implications for generative linguistics of the current functioning of large language models.

Old and New Minimalism: a Hopf algebra comparison

In this paper we compare some old formulations of Minimalism, in particular Stabler's computational minimalism, and Chomsky's new formulation of Merge and Minimalism, from the point of view of their mathematical description in terms of Hopf algebras. We show that the newer formulation has a clear advantage purely in terms of the underlying mathematical structure. More precisely, in the case of Stabler's computational minimalism, External Merge can be described in terms of a partially defined operated algebra with binary operation, while Internal Merge determines a system of right-ideal coideals of the Loday-Ronco Hopf algebra and corresponding right-module coalgebra quotients. This mathematical structure shows that Internal and External Merge have significantly different roles in the old formulations of Minimalism, and they are more difficult to reconcile as facets of a single algebraic operation, as desirable linguistically. On the other hand, we show that the newer formulation of Minimalism naturally carries a Hopf algebra structure where Internal and External Merge directly arise from the same operation. We also compare, at the level of algebraic properties, the externalization model of the new Minimalism with proposals for assignments of planar embeddings based on heads of trees.

On the Computational Power of RNNs

Recent neural network architectures such as the basic recurrent neural network (RNN) and Gated Recurrent Unit (GRU) have gained prominence as end-to-end learning architectures for natural language processing tasks. But what is the computational power of such systems? We prove that finite precision RNNs with one hidden layer and ReLU activation and finite precision GRUs are exactly as computationally powerful as deterministic finite automata. Allowing arbitrary precision, we prove that RNNs with one hidden layer and ReLU activation are at least as computationally powerful as pushdown automata. If we also allow infinite precision, infinite edge weights, and nonlinear output activation functions, we prove that GRUs are at least as computationally powerful as pushdown automata. All results are shown constructively.

Evaluating the Ability of LSTMs to Learn Context-Free Grammars

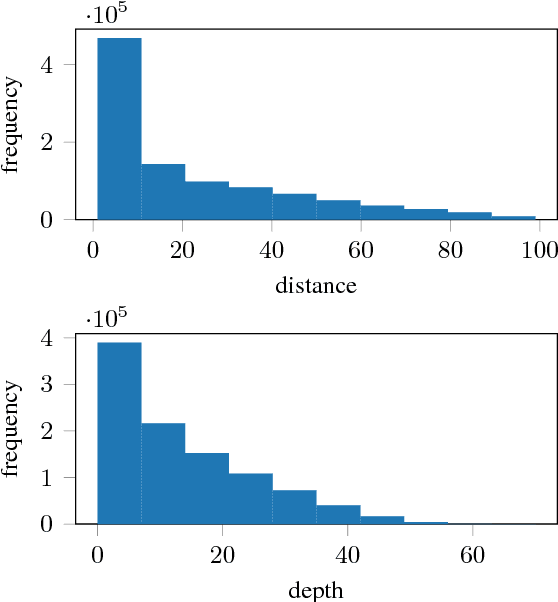
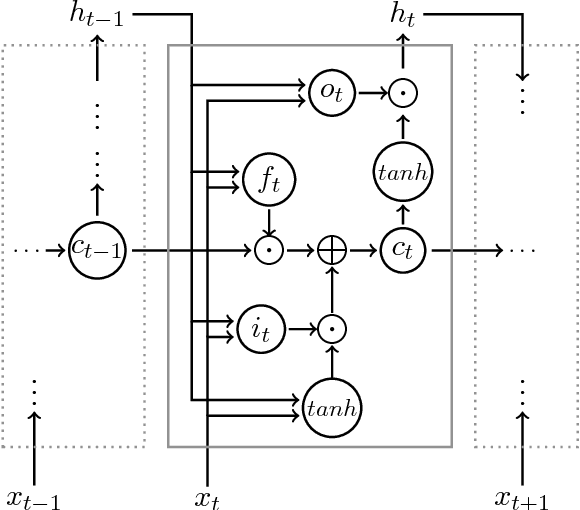
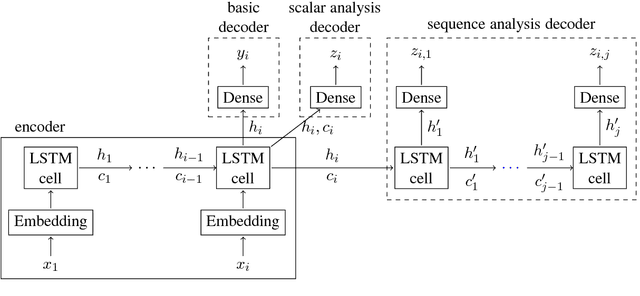
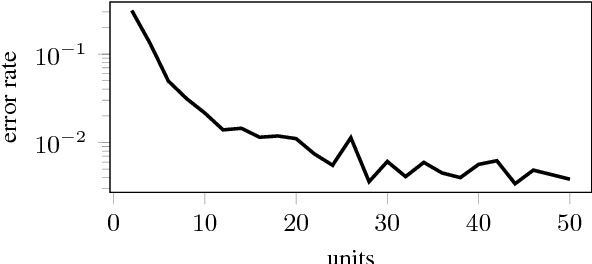
While long short-term memory (LSTM) neural net architectures are designed to capture sequence information, human language is generally composed of hierarchical structures. This raises the question as to whether LSTMs can learn hierarchical structures. We explore this question with a well-formed bracket prediction task using two types of brackets modeled by an LSTM. Demonstrating that such a system is learnable by an LSTM is the first step in demonstrating that the entire class of CFLs is also learnable. We observe that the model requires exponential memory in terms of the number of characters and embedded depth, where a sub-linear memory should suffice. Still, the model does more than memorize the training input. It learns how to distinguish between relevant and irrelevant information. On the other hand, we also observe that the model does not generalize well. We conclude that LSTMs do not learn the relevant underlying context-free rules, suggesting the good overall performance is attained rather by an efficient way of evaluating nuisance variables. LSTMs are a way to quickly reach good results for many natural language tasks, but to understand and generate natural language one has to investigate other concepts that can make more direct use of natural language's structural nature.

Heat Kernel analysis of Syntactic Structures

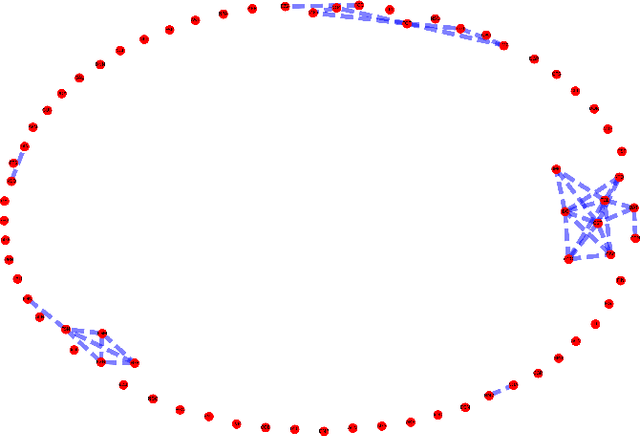
We consider two different data sets of syntactic parameters and we discuss how to detect relations between parameters through a heat kernel method developed by Belkin-Niyogi, which produces low dimensional representations of the data, based on Laplace eigenfunctions, that preserve neighborhood information. We analyze the different connectivity and clustering structures that arise in the two datasets, and the regions of maximal variance in the two-parameter space of the Belkin-Niyogi construction, which identify preferable choices of independent variables. We compute clustering coefficients and their variance.

A Note on Zipf's Law, Natural Languages, and Noncoding DNA regions

In Phys. Rev. Letters (73:2, 5 Dec. 94), Mantegna et al. conclude on the basis of Zipf rank frequency data that noncoding DNA sequence regions are more like natural languages than coding regions. We argue on the contrary that an empirical fit to Zipf's ``law'' cannot be used as a criterion for similarity to natural languages. Although DNA is a presumably an ``organized system of signs'' in Mandelbrot's (1961) sense, an observation of statistical features of the sort presented in the Mantegna et al. paper does not shed light on the similarity between DNA's ``grammar'' and natural language grammars, just as the observation of exact Zipf-like behavior cannot distinguish between the underlying processes of tossing an $M$ sided die or a finite-state branching process.