Heat Kernel analysis of Syntactic Structures
Paper and Code
Mar 26, 2018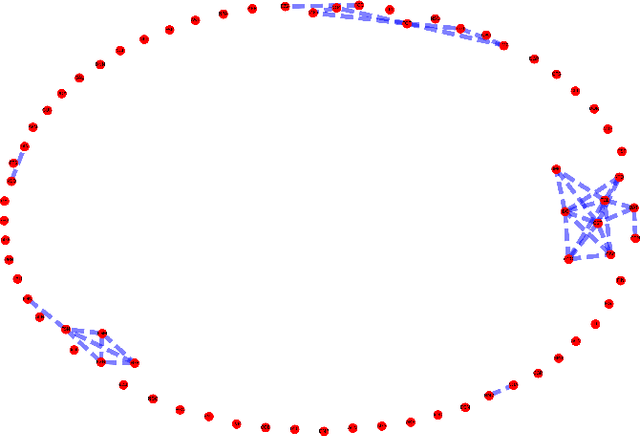

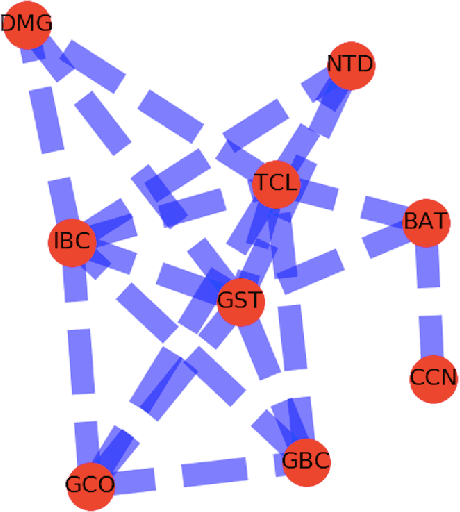

We consider two different data sets of syntactic parameters and we discuss how to detect relations between parameters through a heat kernel method developed by Belkin-Niyogi, which produces low dimensional representations of the data, based on Laplace eigenfunctions, that preserve neighborhood information. We analyze the different connectivity and clustering structures that arise in the two datasets, and the regions of maximal variance in the two-parameter space of the Belkin-Niyogi construction, which identify preferable choices of independent variables. We compute clustering coefficients and their variance.
* 20 pages, LaTeX, png figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge