Merge on workspaces as Hopf algebra Markov chain

We study the dynamical properties of a Hopf algebra Markov chain with state space the binary rooted forests with labelled leaves. This Markovian dynamical system describes the core computational process of structure formation and transformation in syntax via the Merge operation, according to Chomsky's Minimalism model of generative linguistics. The dynamics decomposes into an ergodic dynamical system with uniform stationary distribution, given by the action of Internal Merge, while the contributions of External Merge and (a minimal form of) Sideward Merge reduce to a simpler Markov chain with state space the set of partitions and with combinatorial weights. The Sideward Merge part of the dynamics prevents convergence to fully formed connected structures (trees), unless the different forms of Merge are weighted by a cost function, as predicted by linguistic theory. Results on the asymptotic behavior of the Perron-Frobenius eigenvalue and eigenvector in this weighted case, obtained in terms of an associated Perron-Frobenius problem in the tropical semiring, show that the usual cost functions (Minimal Search and Resource Restrictions) proposed in the linguistic literature do not suffice to obtain convergence to the tree structures, while an additional optimization property based on the Shannon entropy achieves the expected result for the dynamics. We also comment on the introduction of continuous parameters related to semantic embedding and other computational models, and also on some filtering of the dynamics by coloring rules that model the linguistic filtering by theta roles and phase structure, and on parametric variation and the process of parameter setting in Externalization.

Encoding syntactic objects and Merge operations in function spaces

We provide a mathematical argument showing that, given a representation of lexical items as functions (wavelets, for instance) in some function space, it is possible to construct a faithful representation of arbitrary syntactic objects in the same function space. This space can be endowed with a commutative non-associative semiring structure built using the second Renyi entropy. The resulting representation of syntactic objects is compatible with the magma structure. The resulting set of functions is an algebra over an operad, where the operations in the operad model circuits that transform the input wave forms into a combined output that encodes the syntactic structure. The action of Merge on workspaces is faithfully implemented as action on these circuits, through a coproduct and a Hopf algebra Markov chain. The results obtained here provide a constructive argument showing the theoretical possibility of a neurocomputational realization of the core computational structure of syntax. We also present a particular case of this general construction where this type of realization of Merge is implemented as a cross frequency phase synchronization on sinusoidal waves. This also shows that Merge can be expressed in terms of the successor function of a semiring, thus clarifying the well known observation of its similarities with the successor function of arithmetic.

Hypermagmas and Colored Operads: Heads, Phases, and Theta Roles

We show that head functions on syntactic objects extend the magma structure to a hypermagma, with the c-command relation compatible with the magma operation and the m-command relation with the hypermagma. We then show that the structure of head and complement and specifier, additional modifier positions, and the structure of phases in the Extended Projection can be formulated as a bud generating system of a colored operad, in a form similar to the structure of theta roles. We also show that, due to the special form of the colored operad generators, the filtering of freely generated syntactic objects by these coloring rules can be equivalently formulated as a filtering in the course of structure formation via a colored Merge, which can in turn be related to the hypermagma structure. The rules on movement by Internal Merge with respect to phases, the Extended Projection Principle, Empty Category Principle, and Phase Impenetrability Condition are all subsumed into the form of the colored operad generators. Movement compatibilities between the phase structure and the theta roles assignments can then be formulated in terms of the respective colored operads and a transduction of colored operads.

Theta Theory: operads and coloring

We give an explicit construction of the generating set of a colored operad that implements theta theory in the mathematical model of Minimalism in generative linguistics, in the form of a coloring algorithm for syntactic objects. We show that the coproduct operation on workspaces allows for a recursive implementation of the theta criterion. We also show that this filtering by coloring rules on structures freely formed by Merge is equivalent to a process of structure formation by a colored version of Merge: the form of the generators of the colored operad then implies the dichotomy is semantics between External and Internal Merge, where Internal Merge only moves to non-theta positions.

Formal Languages and TQFTs with Defects

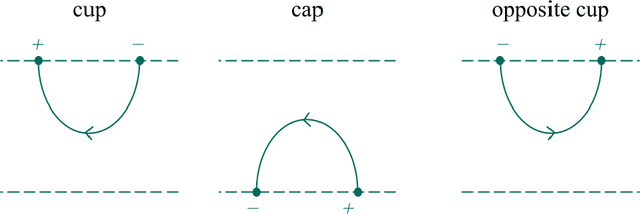
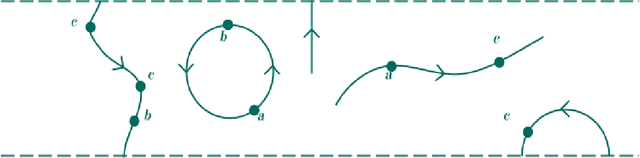
A construction that assigns a Boolean 1D TQFT with defects to a finite state automaton was recently developed by Gustafson, Im, Kaldawy, Khovanov, and Lihn. We show that the construction is functorial with respect to the category of finite state automata with transducers as morphisms. Certain classes of subregular languages correspond to additional cohomological structures on the associated TQFTs. We also show that the construction generalizes to context-free grammars through a categorical version of the Chomsky-Sch\"utzenberger representation theorem, due to Melli\`es and Zeilberger. The corresponding TQFTs are then described as morphisms of colored operads on an operad of cobordisms with defects.

Syntax-semantics interface: an algebraic model

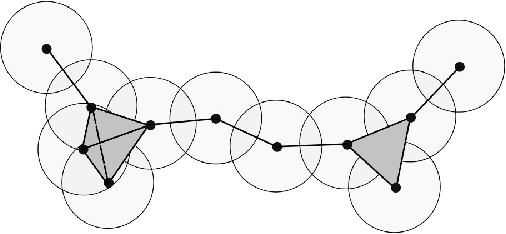
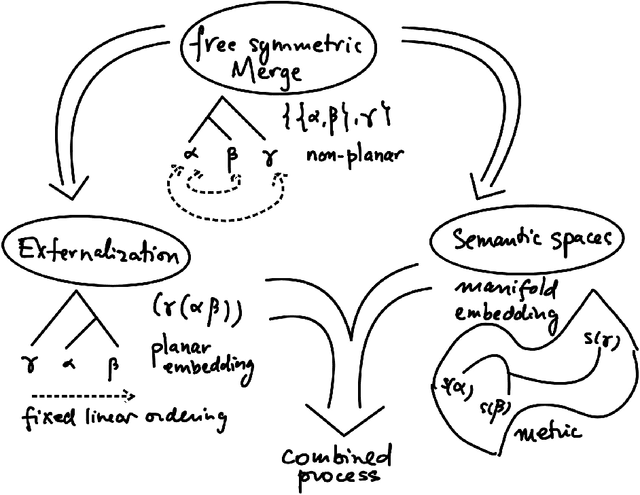
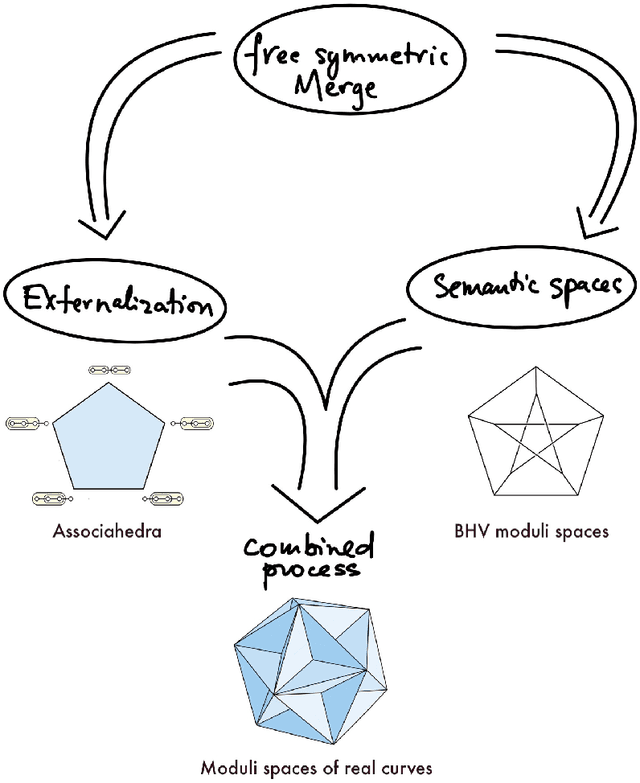
We extend our formulation of Merge and Minimalism in terms of Hopf algebras to an algebraic model of a syntactic-semantic interface. We show that methods adopted in the formulation of renormalization (extraction of meaningful physical values) in theoretical physics are relevant to describe the extraction of meaning from syntactic expressions. We show how this formulation relates to computational models of semantics and we answer some recent controversies about implications for generative linguistics of the current functioning of large language models.

Gabor frames and higher dimensional boundaries in signal analysis on manifolds

We provide a construction of Gabor frames that encode local linearizations of a signal detected on a curved smooth manifold of arbitrary dimension, with Gabor filters that can detect the presence of higher-dimensional boundaries in the manifold signal. We describe an application in configuration spaces in robotics with sharp constrains. The construction is a higher-dimensional generalization of the geometric setting developed for the study of signal analysis in the visual cortex.

Old and New Minimalism: a Hopf algebra comparison

In this paper we compare some old formulations of Minimalism, in particular Stabler's computational minimalism, and Chomsky's new formulation of Merge and Minimalism, from the point of view of their mathematical description in terms of Hopf algebras. We show that the newer formulation has a clear advantage purely in terms of the underlying mathematical structure. More precisely, in the case of Stabler's computational minimalism, External Merge can be described in terms of a partially defined operated algebra with binary operation, while Internal Merge determines a system of right-ideal coideals of the Loday-Ronco Hopf algebra and corresponding right-module coalgebra quotients. This mathematical structure shows that Internal and External Merge have significantly different roles in the old formulations of Minimalism, and they are more difficult to reconcile as facets of a single algebraic operation, as desirable linguistically. On the other hand, we show that the newer formulation of Minimalism naturally carries a Hopf algebra structure where Internal and External Merge directly arise from the same operation. We also compare, at the level of algebraic properties, the externalization model of the new Minimalism with proposals for assignments of planar embeddings based on heads of trees.

Mathematical Structure of Syntactic Merge

The syntactic Merge operation of the Minimalist Program in linguistics can be described mathematically in terms of Hopf algebras, with a formalism similar to the one arising in the physics of renormalization. This mathematical formulation of Merge has good descriptive power, as phenomena empirically observed in linguistics can be justified from simple mathematical arguments. It also provides a possible mathematical model for externalization and for the role of syntactic parameters.

Syntactic structures and the general Markov models

We further the theme of studying syntactic structures data from Longobardi (2017b), Collins (2010), Ceolin et al. (2020) and Koopman (2011) using general Markov models initiated in Shu et al. (2017), exploring the question of how consistent the data is with the idea that general Markov models. The ideas explored in the present paper are more generally applicable than to the setting of syntactic structures, and can be used when analyzing consistency of data with general Markov models. Additionally, we give an interpretation of the methods of Ceolin et al. (2020) as an infinite sites evolutionary model and compare it to the Markov model and explore each in the context of evolutionary processes acting on human language syntax.