Formal Languages and TQFTs with Defects
Paper and Code
Dec 12, 2024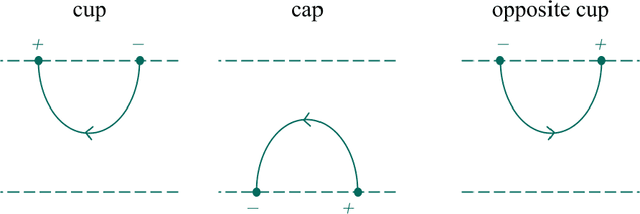
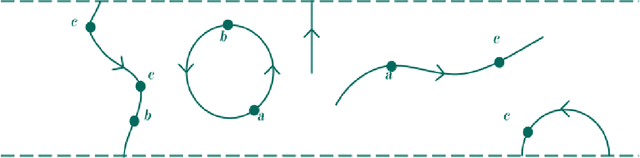

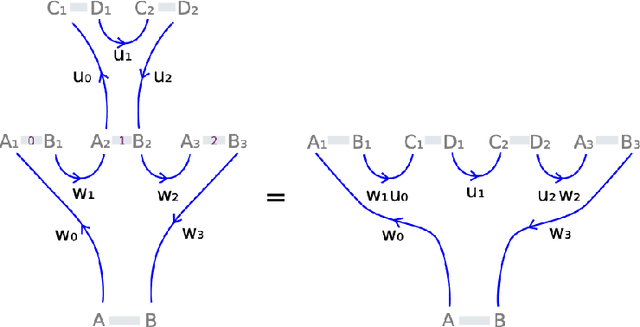
A construction that assigns a Boolean 1D TQFT with defects to a finite state automaton was recently developed by Gustafson, Im, Kaldawy, Khovanov, and Lihn. We show that the construction is functorial with respect to the category of finite state automata with transducers as morphisms. Certain classes of subregular languages correspond to additional cohomological structures on the associated TQFTs. We also show that the construction generalizes to context-free grammars through a categorical version of the Chomsky-Sch\"utzenberger representation theorem, due to Melli\`es and Zeilberger. The corresponding TQFTs are then described as morphisms of colored operads on an operad of cobordisms with defects.
* 28 pages, 9 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge