Heat Kernel analysis of Syntactic Structures

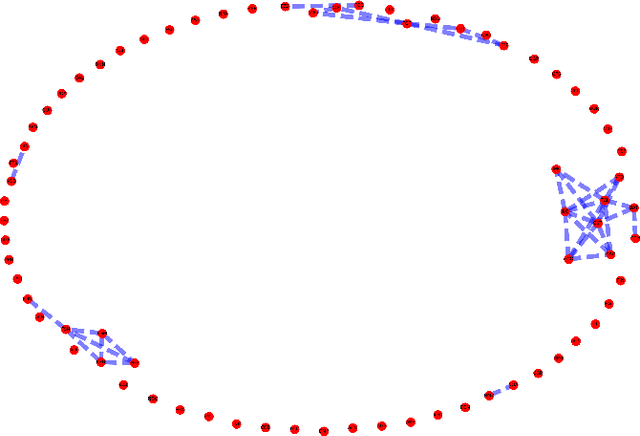
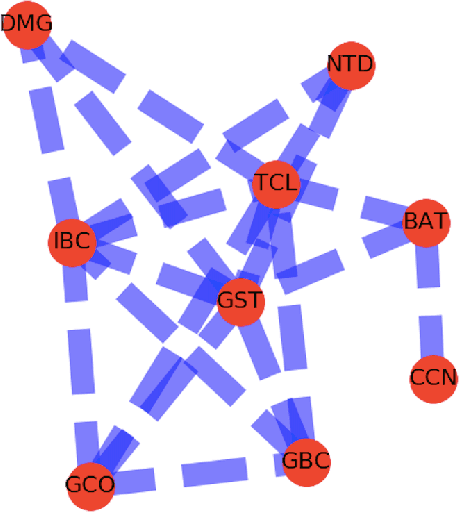
We consider two different data sets of syntactic parameters and we discuss how to detect relations between parameters through a heat kernel method developed by Belkin-Niyogi, which produces low dimensional representations of the data, based on Laplace eigenfunctions, that preserve neighborhood information. We analyze the different connectivity and clustering structures that arise in the two datasets, and the regions of maximal variance in the two-parameter space of the Belkin-Niyogi construction, which identify preferable choices of independent variables. We compute clustering coefficients and their variance.

Phylogenetics of Indo-European Language families via an Algebro-Geometric Analysis of their Syntactic Structures

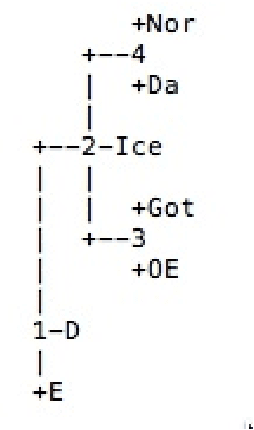
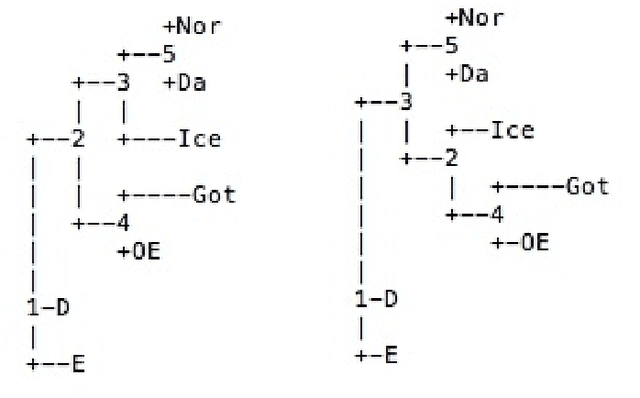
Using Phylogenetic Algebraic Geometry, we analyze computationally the phylogenetic tree of subfamilies of the Indo-European language family, using data of syntactic structures. The two main sources of syntactic data are the SSWL database and Longobardi's recent data of syntactic parameters. We compute phylogenetic invariants and likelihood functions for two sets of Germanic languages, a set of Romance languages, a set of Slavic languages and a set of early Indo-European languages, and we compare the results with what is known through historical linguistics.