Phylogenetics of Indo-European Language families via an Algebro-Geometric Analysis of their Syntactic Structures

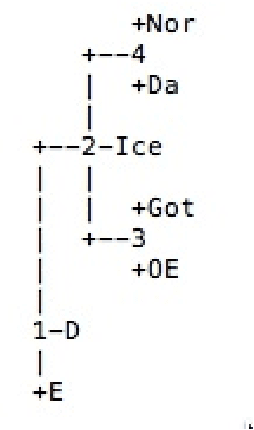
Using Phylogenetic Algebraic Geometry, we analyze computationally the phylogenetic tree of subfamilies of the Indo-European language family, using data of syntactic structures. The two main sources of syntactic data are the SSWL database and Longobardi's recent data of syntactic parameters. We compute phylogenetic invariants and likelihood functions for two sets of Germanic languages, a set of Romance languages, a set of Slavic languages and a set of early Indo-European languages, and we compare the results with what is known through historical linguistics.

Syntactic Structures and Code Parameters

We assign binary and ternary error-correcting codes to the data of syntactic structures of world languages and we study the distribution of code points in the space of code parameters. We show that, while most codes populate the lower region approximating a superposition of Thomae functions, there is a substantial presence of codes above the Gilbert-Varshamov bound and even above the asymptotic bound and the Plotkin bound. We investigate the dynamics induced on the space of code parameters by spin glass models of language change, and show that, in the presence of entailment relations between syntactic parameters the dynamics can sometimes improve the code. For large sets of languages and syntactic data, one can gain information on the spin glass dynamics from the induced dynamics in the space of code parameters.

Syntactic Phylogenetic Trees

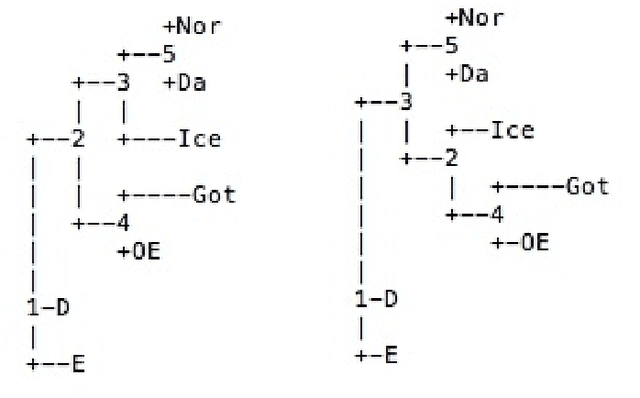
In this paper we identify several serious problems that arise in the use of syntactic data from the SSWL database for the purpose of computational phylogenetic reconstruction. We show that the most naive approach fails to produce reliable linguistic phylogenetic trees. We identify some of the sources of the observed problems and we discuss how they may be, at least partly, corrected by using additional information, such as prior subdivision into language families and subfamilies, and a better use of the information about ancient languages. We also describe how the use of phylogenetic algebraic geometry can help in estimating to what extent the probability distribution at the leaves of the phylogenetic tree obtained from the SSWL data can be considered reliable, by testing it on phylogenetic trees established by other forms of linguistic analysis. In simple examples, we find that, after restricting to smaller language subfamilies and considering only those SSWL parameters that are fully mapped for the whole subfamily, the SSWL data match extremely well reliable phylogenetic trees, according to the evaluation of phylogenetic invariants. This is a promising sign for the use of SSWL data for linguistic phylogenetics.