Series-to-Series Diffusion Bridge Model

Diffusion models have risen to prominence in time series forecasting, showcasing their robust capability to model complex data distributions. However, their effectiveness in deterministic predictions is often constrained by instability arising from their inherent stochasticity. In this paper, we revisit time series diffusion models and present a comprehensive framework that encompasses most existing diffusion-based methods. Building on this theoretical foundation, we propose a novel diffusion-based time series forecasting model, the Series-to-Series Diffusion Bridge Model ($\mathrm{S^2DBM}$), which leverages the Brownian Bridge process to reduce randomness in reverse estimations and improves accuracy by incorporating informative priors and conditions derived from historical time series data. Experimental results demonstrate that $\mathrm{S^2DBM}$ delivers superior performance in point-to-point forecasting and competes effectively with other diffusion-based models in probabilistic forecasting.

IGNN-Solver: A Graph Neural Solver for Implicit Graph Neural Networks

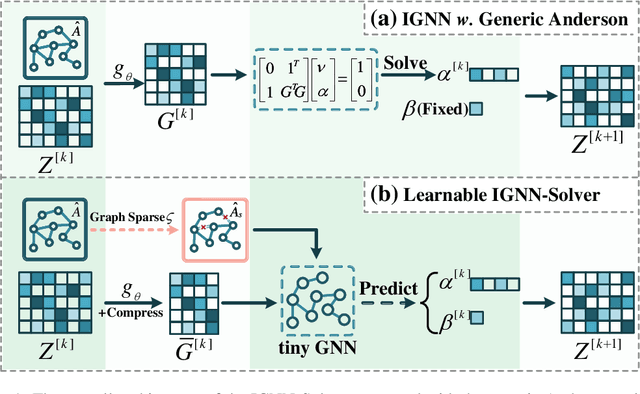
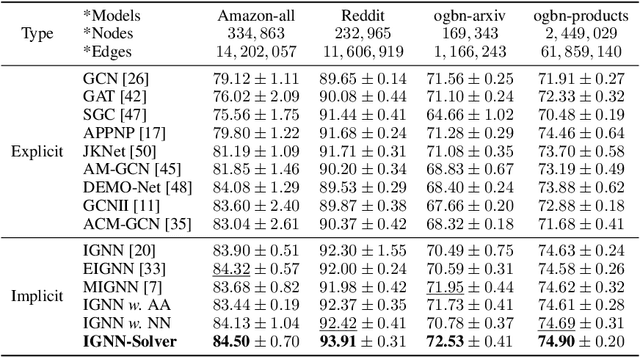
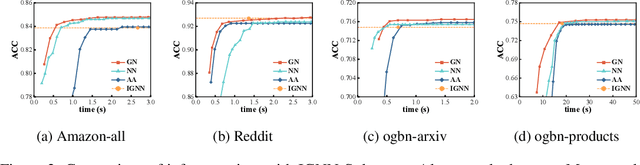
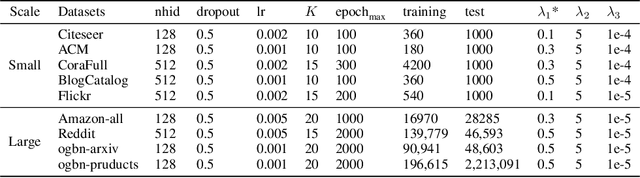
Implicit graph neural networks (IGNNs), which exhibit strong expressive power with a single layer, have recently demonstrated remarkable performance in capturing long-range dependencies (LRD) in underlying graphs while effectively mitigating the over-smoothing problem. However, IGNNs rely on computationally expensive fixed-point iterations, which lead to significant speed and scalability limitations, hindering their application to large-scale graphs. To achieve fast fixed-point solving for IGNNs, we propose a novel graph neural solver, IGNN-Solver, which leverages the generalized Anderson Acceleration method, parameterized by a small GNN, and learns iterative updates as a graph-dependent temporal process. Extensive experiments demonstrate that the IGNN-Solver significantly accelerates inference, achieving a $1.5\times$ to $8\times$ speedup without sacrificing accuracy. Moreover, this advantage becomes increasingly pronounced as the graph scale grows, facilitating its large-scale deployment in real-world applications.