Consistency Deep Equilibrium Models

Deep Equilibrium Models (DEQs) have emerged as a powerful paradigm in deep learning, offering the ability to model infinite-depth networks with constant memory usage. However, DEQs incur significant inference latency due to the iterative nature of fixed-point solvers. In this work, we introduce the Consistency Deep Equilibrium Model (C-DEQ), a novel framework that leverages consistency distillation to accelerate DEQ inference. We cast the DEQ iterative inference process as evolution along a fixed ODE trajectory toward the equilibrium. Along this trajectory, we train C-DEQs to consistently map intermediate states directly to the fixed point, enabling few-step inference while preserving the performance of the teacher DEQ. At the same time, it facilitates multi-step evaluation to flexibly trade computation for performance gains. Extensive experiments across various domain tasks demonstrate that C-DEQs achieves consistent 2-20$\times$ accuracy improvements over implicit DEQs under the same few-step inference budget.

IGNN-Solver: A Graph Neural Solver for Implicit Graph Neural Networks

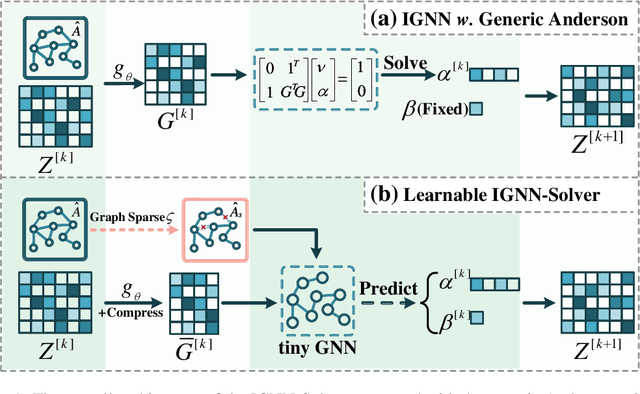
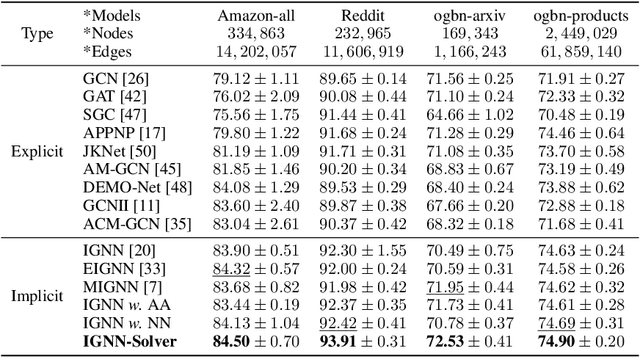
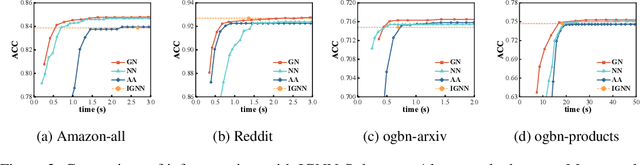
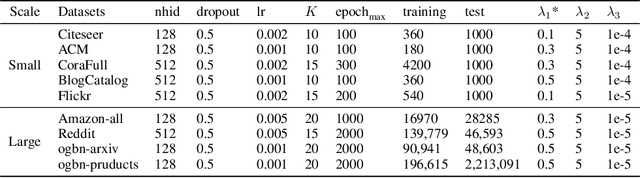
Implicit graph neural networks (IGNNs), which exhibit strong expressive power with a single layer, have recently demonstrated remarkable performance in capturing long-range dependencies (LRD) in underlying graphs while effectively mitigating the over-smoothing problem. However, IGNNs rely on computationally expensive fixed-point iterations, which lead to significant speed and scalability limitations, hindering their application to large-scale graphs. To achieve fast fixed-point solving for IGNNs, we propose a novel graph neural solver, IGNN-Solver, which leverages the generalized Anderson Acceleration method, parameterized by a small GNN, and learns iterative updates as a graph-dependent temporal process. Extensive experiments demonstrate that the IGNN-Solver significantly accelerates inference, achieving a $1.5\times$ to $8\times$ speedup without sacrificing accuracy. Moreover, this advantage becomes increasingly pronounced as the graph scale grows, facilitating its large-scale deployment in real-world applications.

Semantic Graph Neural Network with Multi-measure Learning for Semi-supervised Classification

Graph Neural Networks (GNNs) have attracted increasing attention in recent years and have achieved excellent performance in semi-supervised node classification tasks. The success of most GNNs relies on one fundamental assumption, i.e., the original graph structure data is available. However, recent studies have shown that GNNs are vulnerable to the complex underlying structure of the graph, making it necessary to learn comprehensive and robust graph structures for downstream tasks, rather than relying only on the raw graph structure. In light of this, we seek to learn optimal graph structures for downstream tasks and propose a novel framework for semi-supervised classification. Specifically, based on the structural context information of graph and node representations, we encode the complex interactions in semantics and generate semantic graphs to preserve the global structure. Moreover, we develop a novel multi-measure attention layer to optimize the similarity rather than prescribing it a priori, so that the similarity can be adaptively evaluated by integrating measures. These graphs are fused and optimized together with GNN towards semi-supervised classification objective. Extensive experiments and ablation studies on six real-world datasets clearly demonstrate the effectiveness of our proposed model and the contribution of each component.