LDPC Decoding with Degree-Specific Neural Message Weights and RCQ Decoding

Recently, neural networks have improved MinSum message-passing decoders for low-density parity-check (LDPC) codes by multiplying or adding weights to the messages, where the weights are determined by a neural network. The neural network complexity to determine distinct weights for each edge is high, often limiting the application to relatively short LDPC codes. Furthermore, storing separate weights for every edge and every iteration can be a burden for hardware implementations. To reduce neural network complexity and storage requirements, this paper proposes a family of weight-sharing schemes that use the same weight for edges that have the same check node degree and/or variable node degree. Our simulation results show that node-degree-based weight-sharing can deliver the same performance requiring distinct weights for each node. This paper also combines these degree-specific neural weights with a reconstruction-computation-quantization (RCQ) decoder to produce a weighted RCQ (W-RCQ) decoder. The W-RCQ decoder with node-degree-based weight sharing has a reduced hardware requirement compared with the original RCQ decoder. As an additional contribution, this paper identifies and resolves a gradient explosion issue that can arise when training neural LDPC decoders.

Achievable Rates and Low-Complexity Encoding of Posterior Matching for the BSC

Horstein, Burnashev, Shayevitz and Feder, Naghshvar et al. and others have studied sequential transmission of a K-bit message over the binary symmetric channel (BSC) with full, noiseless feedback using posterior matching. Yang et al. provide an improved lower bound on the achievable rate using martingale analysis that relies on the small-enough difference (SED) partitioning introduced by Naghshvar et al. SED requires a relatively complex encoder and decoder. To reduce complexity, this paper replaces SED with relaxed constraints that admit the small enough absolute difference (SEAD) partitioning rule. The main analytical results show that achievable-rate bounds higher than those found by Yang et al. are possible even under the new constraints, which are less restrictive than SED. The new analysis does not use martingale theory for the confirmation phase and applies a surrogate channel technique to tighten the results. An initial systematic transmission further increases the achievable rate bound. The simplified encoder associated with SEAD has a complexity below order O(K^2) and allows simulations for message sizes of at least 1000 bits. For example, simulations achieve 99% of of the channel's 0.50-bit capacity with an average block size of 200 bits for a target codeword error rate of 10^(-3).

Reconstruction-Computation-Quantization (RCQ): A Paradigm for Low Bit Width LDPC Decoding

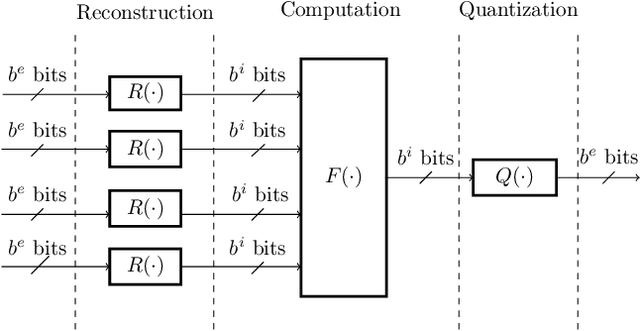
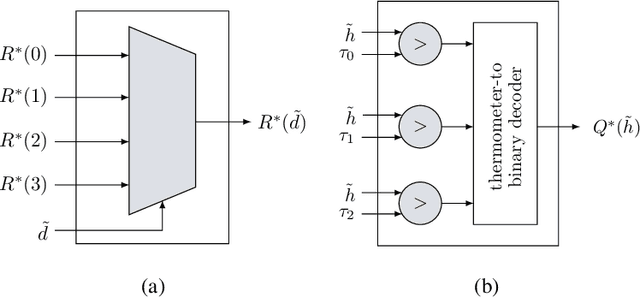
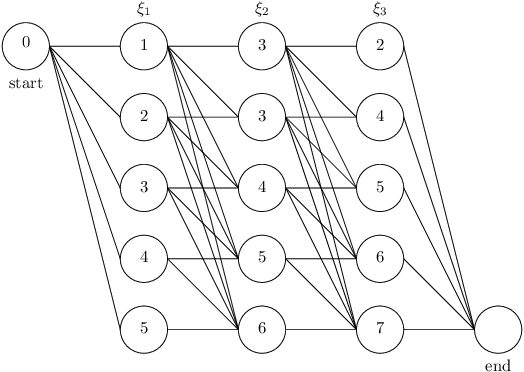
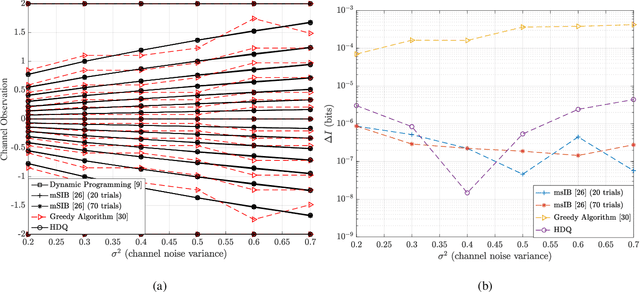
This paper uses the reconstruction-computation-quantization (RCQ) paradigm to decode low-density parity-check (LDPC) codes. RCQ facilitates dynamic non-uniform quantization to achieve good frame error rate (FER) performance with very low message precision. For message-passing according to a flooding schedule, the RCQ parameters are designed by discrete density evolution (DDE). Simulation results on an IEEE 802.11 LDPC code show that for 4-bit messages, a flooding MinSum RCQ decoder outperforms table-lookup approaches such as information bottleneck (IB) or Min-IB decoding, with significantly fewer parameters to be stored. Additionally, this paper introduces layer-specific RCQ (LS-RCQ), an extension of RCQ decoding for layered architectures. LS-RCQ uses layer-specific message representations to achieve the best possible FER performance. For LS-RCQ, this paper proposes using layered DDE featuring hierarchical dynamic quantization (HDQ) to design LS-RCQ parameters efficiently. Finally, this paper studies field-programmable gate array (FPGA) implementations of RCQ decoders. Simulation results for a (9472, 8192) quasi-cyclic (QC) LDPC code show that a layered MinSum RCQ decoder with 3-bit messages achieves more than a $10\%$ reduction in LUTs and routed nets and more than a $6\%$ decrease in register usage while maintaining comparable decoding performance, compared to a 5-bit offset MinSum decoder.

FPGA Implementations of Layered MinSum LDPC Decoders Using RCQ Message Passing

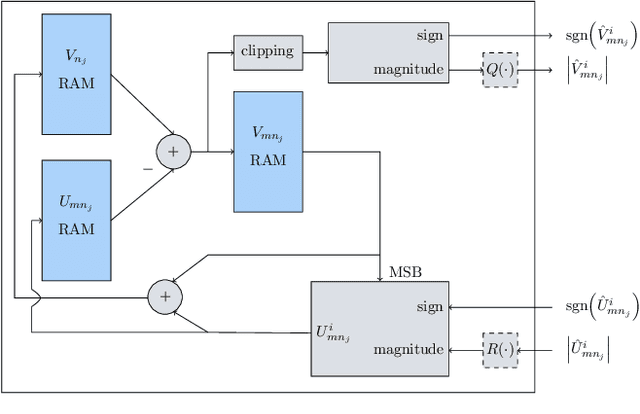
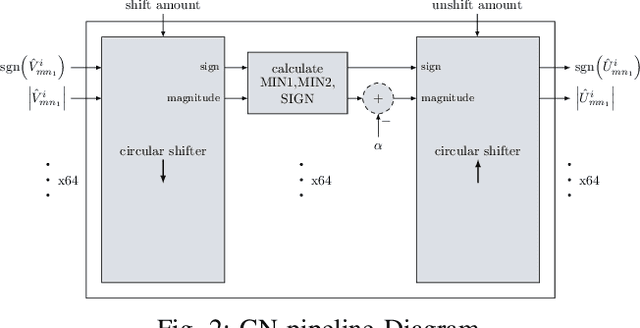
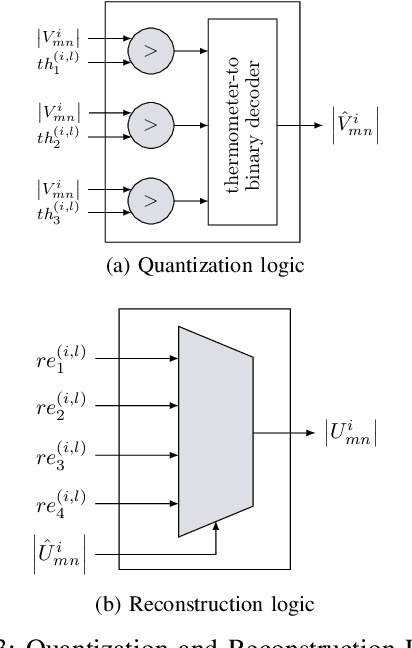
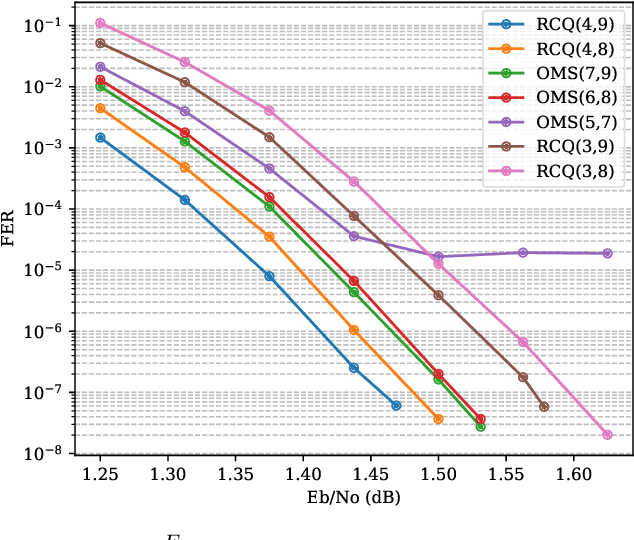
Non-uniform message quantization techniques such as reconstruction-computation-quantization (RCQ) improve error-correction performance and decrease hardware complexity of low-density parity-check (LDPC) decoders that use a flooding schedule. Layered MinSum RCQ (L-msRCQ) enables message quantization to be utilized for layered decoders and irregular LDPC codes. We investigate field-programmable gate array (FPGA) implementations of L-msRCQ decoders. Three design methods for message quantization are presented, which we name the Lookup, Broadcast, and Dribble methods. The decoding performance and hardware complexity of these schemes are compared to a layered offset MinSum (OMS) decoder. Simulation results on a (16384, 8192) protograph-based raptor-like (PBRL) LDPC code show that a 4-bit L-msRCQ decoder using the Broadcast method can achieve a 0.03 dB improvement in error-correction performance while using 12% fewer registers than the OMS decoder. A Broadcast-based 3-bit L-msRCQ decoder uses 15% fewer lookup tables, 18% fewer registers, and 13% fewer routed nets than the OMS decoder, but results in a 0.09 dB loss in performance.