Reconstruction-Computation-Quantization (RCQ): A Paradigm for Low Bit Width LDPC Decoding

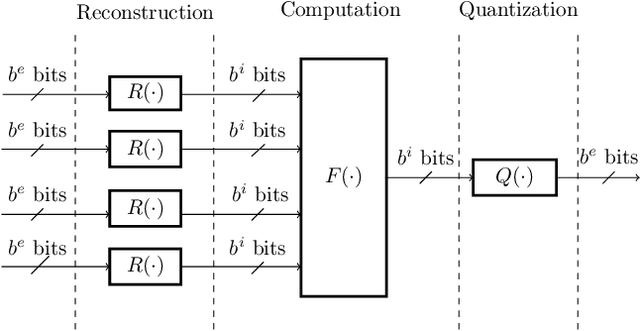
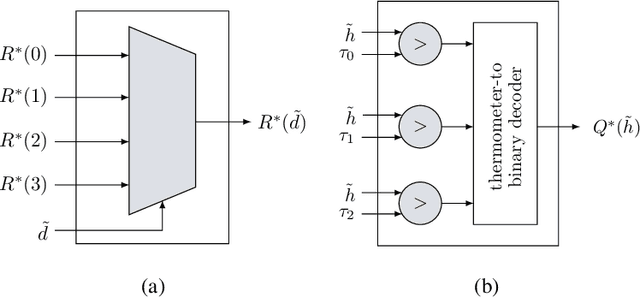
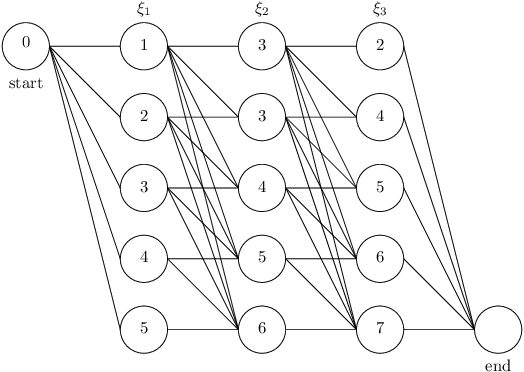
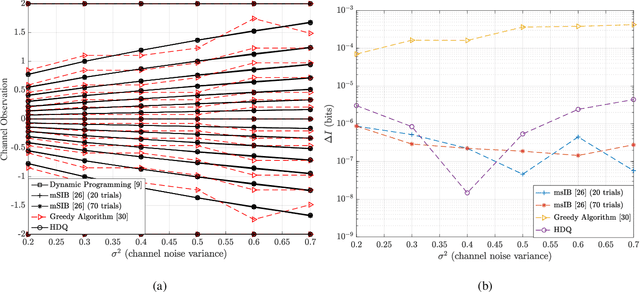
This paper uses the reconstruction-computation-quantization (RCQ) paradigm to decode low-density parity-check (LDPC) codes. RCQ facilitates dynamic non-uniform quantization to achieve good frame error rate (FER) performance with very low message precision. For message-passing according to a flooding schedule, the RCQ parameters are designed by discrete density evolution (DDE). Simulation results on an IEEE 802.11 LDPC code show that for 4-bit messages, a flooding MinSum RCQ decoder outperforms table-lookup approaches such as information bottleneck (IB) or Min-IB decoding, with significantly fewer parameters to be stored. Additionally, this paper introduces layer-specific RCQ (LS-RCQ), an extension of RCQ decoding for layered architectures. LS-RCQ uses layer-specific message representations to achieve the best possible FER performance. For LS-RCQ, this paper proposes using layered DDE featuring hierarchical dynamic quantization (HDQ) to design LS-RCQ parameters efficiently. Finally, this paper studies field-programmable gate array (FPGA) implementations of RCQ decoders. Simulation results for a (9472, 8192) quasi-cyclic (QC) LDPC code show that a layered MinSum RCQ decoder with 3-bit messages achieves more than a $10\%$ reduction in LUTs and routed nets and more than a $6\%$ decrease in register usage while maintaining comparable decoding performance, compared to a 5-bit offset MinSum decoder.

FPGA Implementations of Layered MinSum LDPC Decoders Using RCQ Message Passing

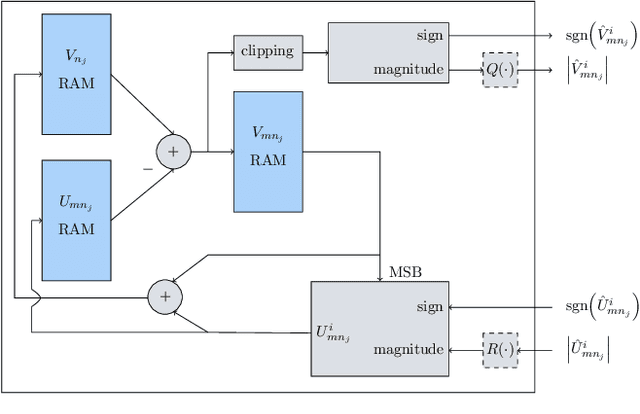
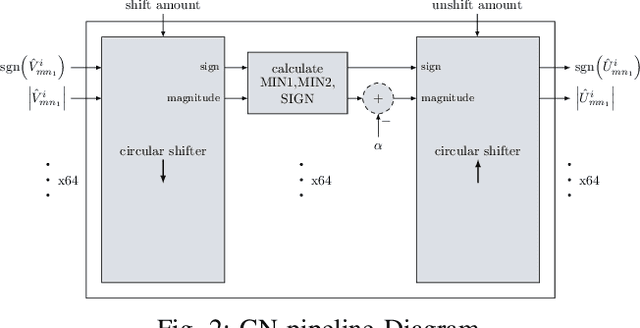
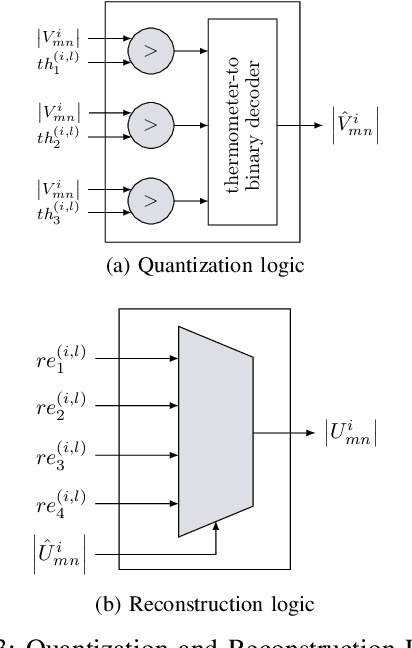
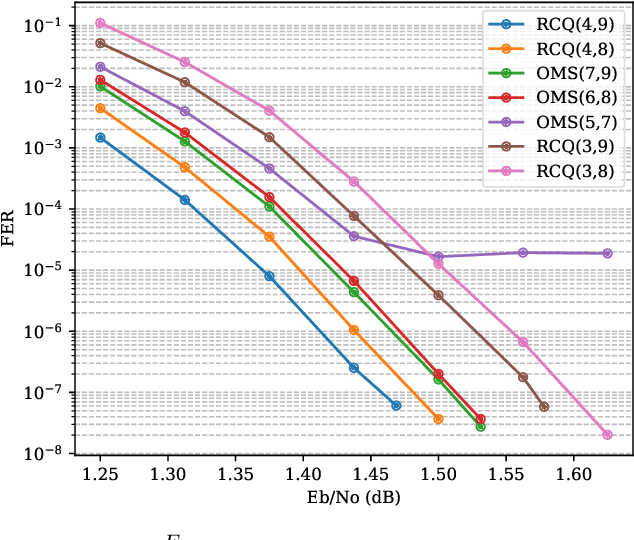
Non-uniform message quantization techniques such as reconstruction-computation-quantization (RCQ) improve error-correction performance and decrease hardware complexity of low-density parity-check (LDPC) decoders that use a flooding schedule. Layered MinSum RCQ (L-msRCQ) enables message quantization to be utilized for layered decoders and irregular LDPC codes. We investigate field-programmable gate array (FPGA) implementations of L-msRCQ decoders. Three design methods for message quantization are presented, which we name the Lookup, Broadcast, and Dribble methods. The decoding performance and hardware complexity of these schemes are compared to a layered offset MinSum (OMS) decoder. Simulation results on a (16384, 8192) protograph-based raptor-like (PBRL) LDPC code show that a 4-bit L-msRCQ decoder using the Broadcast method can achieve a 0.03 dB improvement in error-correction performance while using 12% fewer registers than the OMS decoder. A Broadcast-based 3-bit L-msRCQ decoder uses 15% fewer lookup tables, 18% fewer registers, and 13% fewer routed nets than the OMS decoder, but results in a 0.09 dB loss in performance.