Opti Code Pro: A Heuristic Search-based Approach to Code Refactoring

This paper presents an approach that evaluates best-first search methods to code refactoring. The motivation for code refactoring could be to improve the design, structure, or implementation of an existing program without changing its functionality. To solve a very specific problem of coupling and cohesion, we propose using heuristic search-based techniques on an approximation of the full code refactoring problem, to guide the refactoring process toward solutions that have high cohesion and low coupling. We evaluated our approach by providing demonstrative examples of the effectiveness of this approach on random state problems and created a tool to implement the algorithm on Java projects.

Learning Reward Machines: A Study in Partially Observable Reinforcement Learning

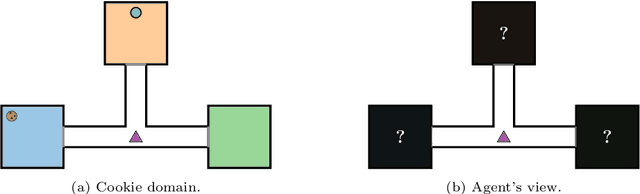
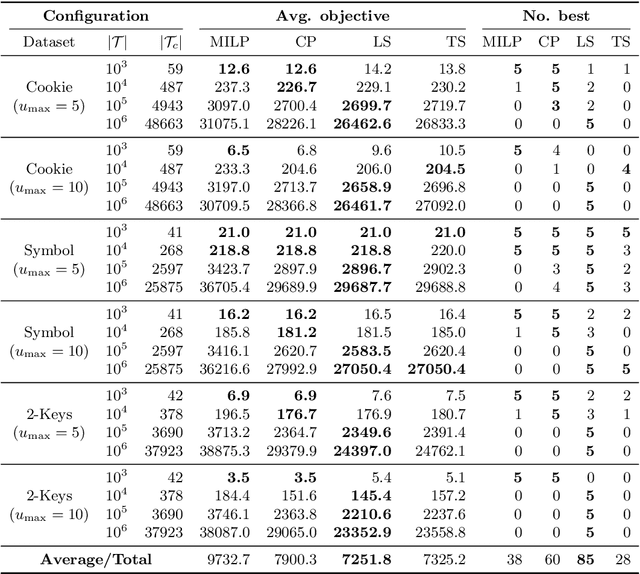
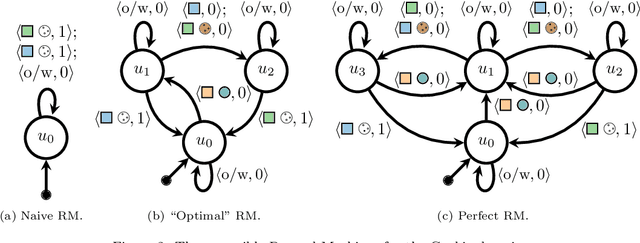
Reinforcement learning (RL) is a central problem in artificial intelligence. This problem consists of defining artificial agents that can learn optimal behaviour by interacting with an environment -- where the optimal behaviour is defined with respect to a reward signal that the agent seeks to maximize. Reward machines (RMs) provide a structured, automata-based representation of a reward function that enables an RL agent to decompose an RL problem into structured subproblems that can be efficiently learned via off-policy learning. Here we show that RMs can be learned from experience, instead of being specified by the user, and that the resulting problem decomposition can be used to effectively solve partially observable RL problems. We pose the task of learning RMs as a discrete optimization problem where the objective is to find an RM that decomposes the problem into a set of subproblems such that the combination of their optimal memoryless policies is an optimal policy for the original problem. We show the effectiveness of this approach on three partially observable domains, where it significantly outperforms A3C, PPO, and ACER, and discuss its advantages, limitations, and broader potential.

Reward Machines: Exploiting Reward Function Structure in Reinforcement Learning

Reinforcement learning (RL) methods usually treat reward functions as black boxes. As such, these methods must extensively interact with the environment in order to discover rewards and optimal policies. In most RL applications, however, users have to program the reward function and, hence, there is the opportunity to treat reward functions as white boxes instead -- to show the reward function's code to the RL agent so it can exploit its internal structures to learn optimal policies faster. In this paper, we show how to accomplish this idea in two steps. First, we propose reward machines (RMs), a type of finite state machine that supports the specification of reward functions while exposing reward function structure. We then describe different methodologies to exploit such structures, including automated reward shaping, task decomposition, and counterfactual reasoning for data augmentation. Experiments on tabular and continuous domains show the benefits of exploiting reward structure across different tasks and RL agents.

The act of remembering: a study in partially observable reinforcement learning

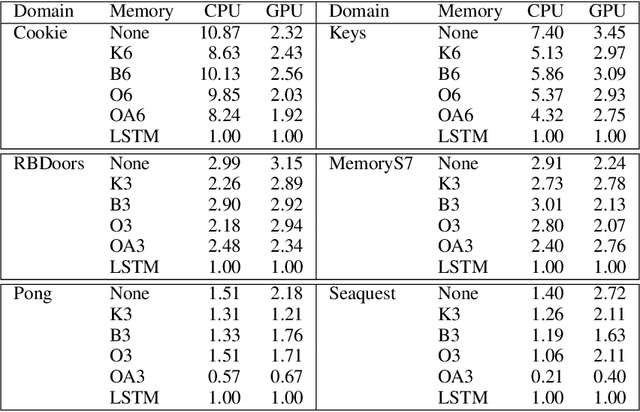
Reinforcement Learning (RL) agents typically learn memoryless policies---policies that only consider the last observation when selecting actions. Learning memoryless policies is efficient and optimal in fully observable environments. However, some form of memory is necessary when RL agents are faced with partial observability. In this paper, we study a lightweight approach to tackle partial observability in RL. We provide the agent with an external memory and additional actions to control what, if anything, is written to the memory. At every step, the current memory state is part of the agent's observation, and the agent selects a tuple of actions: one action that modifies the environment and another that modifies the memory. When the external memory is sufficiently expressive, optimal memoryless policies yield globally optimal solutions. Unfortunately, previous attempts to use external memory in the form of binary memory have produced poor results in practice. Here, we investigate alternative forms of memory in support of learning effective memoryless policies. Our novel forms of memory outperform binary and LSTM-based memory in well-established partially observable domains.