Domain Influence in MRI Medical Image Segmentation: spatial versus k-space inputs

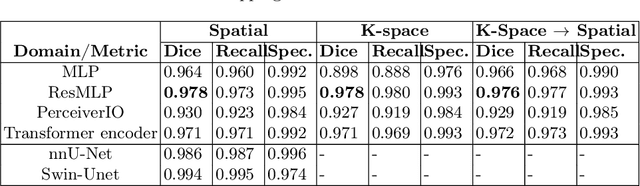
Transformer-based networks applied to image patches have achieved cutting-edge performance in many vision tasks. However, lacking the built-in bias of convolutional neural networks (CNN) for local image statistics, they require large datasets and modifications to capture relationships between patches, especially in segmentation tasks. Images in the frequency domain might be more suitable for the attention mechanism, as local features are represented globally. By transforming images into the frequency domain, local features are represented globally. Due to MRI data acquisition properties, these images are particularly suitable. This work investigates how the image domain (spatial or k-space) affects segmentation results of deep learning (DL) models, focusing on attention-based networks and other non-convolutional models based on MLPs. We also examine the necessity of additional positional encoding for Transformer-based networks when input images are in the frequency domain. For evaluation, we pose a skull stripping task and a brain tissue segmentation task. The attention-based models used are PerceiverIO and a vanilla Transformer encoder. To compare with non-attention-based models, an MLP and ResMLP are also trained and tested. Results are compared with the Swin-Unet, the state-of-the-art medical image segmentation model. Experimental results show that using k-space for the input domain can significantly improve segmentation results. Also, additional positional encoding does not seem beneficial for attention-based networks if the input is in the frequency domain. Although none of the models matched the Swin-Unet's performance, the less complex models showed promising improvements with a different domain choice.

Competitive Algorithms for Online Budget-Constrained Continuous DR-Submodular Problems

In this paper, we study a certain class of online optimization problems, where the goal is to maximize a function that is not necessarily concave and satisfies the Diminishing Returns (DR) property under budget constraints. We analyze a primal-dual algorithm, called the Generalized Sequential algorithm, and we obtain the first bound on the competitive ratio of online monotone DR-submodular function maximization subject to linear packing constraints which matches the known tight bound in the special case of linear objective function.

Exponentiated Subgradient Algorithm for Online Optimization under the Random Permutation Model

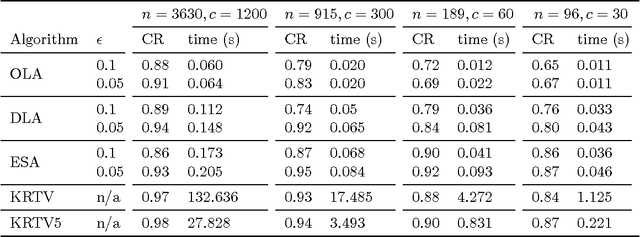
Online optimization problems arise in many resource allocation tasks, where the future demands for each resource and the associated utility functions change over time and are not known apriori, yet resources need to be allocated at every point in time despite the future uncertainty. In this paper, we consider online optimization problems with general concave utilities. We modify and extend an online optimization algorithm proposed by Devanur et al. for linear programming to this general setting. The model we use for the arrival of the utilities and demands is known as the random permutation model, where a fixed collection of utilities and demands are presented to the algorithm in random order. We prove that under this model the algorithm achieves a competitive ratio of $1-O(\epsilon)$ under a near-optimal assumption that the bid to budget ratio is $O (\frac{\epsilon^2}{\log({m}/{\epsilon})})$, where $m$ is the number of resources, while enjoying a significantly lower computational cost than the optimal algorithm proposed by Kesselheim et al. We draw a connection between the proposed algorithm and subgradient methods used in convex optimization. In addition, we present numerical experiments that demonstrate the performance and speed of this algorithm in comparison to existing algorithms.