Differential 2D Copula Approximating Transforms via Sobolev Training: 2-Cats Networks

Copulas are a powerful statistical tool that captures dependencies across data dimensions. When applying Copulas, we can estimate multivariate distribution functions by initially estimating independent marginals, an easy task, and then a single copulating function, $C$, to connect the marginals, a hard task. For two-dimensional data, a copula is a two-increasing function of the form $C: (u,v)\in \mathbf{I}^2 \rightarrow \mathbf{I}$, where $\mathbf{I} = [0, 1]$. In this paper, we show how Neural Networks (NNs) can approximate any two-dimensional copula non-parametrically. Our approach, denoted as 2-Cats, is inspired by the Physics-Informed Neural Networks and Sobolev Training literature. Not only do we show that we can estimate the output of a 2d Copula better than the state-of-the-art, our approach is non-parametric and respects the mathematical properties of a Copula $C$.

Cooperative Object Transportation using Gibbs Random Fields

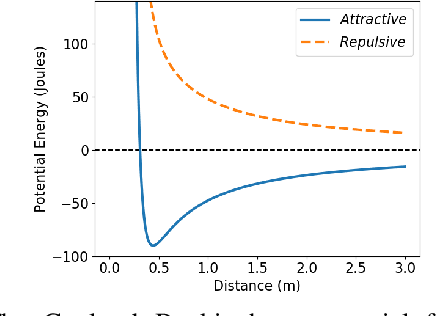
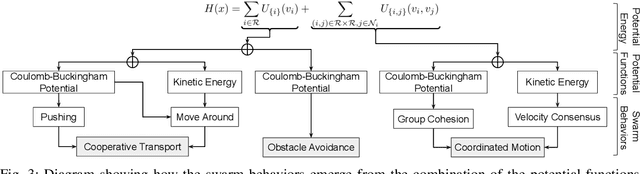
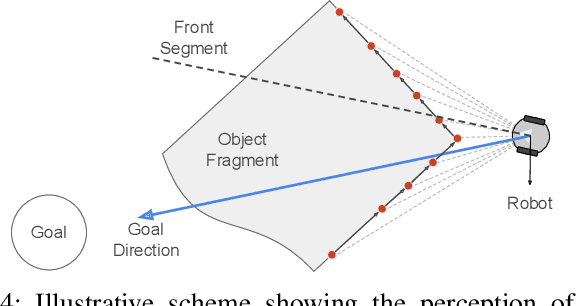
This paper presents a novel methodology that allows a swarm of robots to perform a cooperative transportation task. Our approach consists of modeling the swarm as a {\em Gibbs Random Field} (GRF), taking advantage of this framework's locality properties. By setting appropriate potential functions, robots can dynamically navigate, form groups, and perform cooperative transportation in a completely decentralized fashion. Moreover, these behaviors emerge from the local interactions without the need for explicit communication or coordination. To evaluate our methodology, we perform a series of simulations and proof-of-concept experiments in different scenarios. Our results show that the method is scalable, adaptable, and robust to failures and changes in the environment.

Fast Estimation of Causal Interactions using Wold Processes

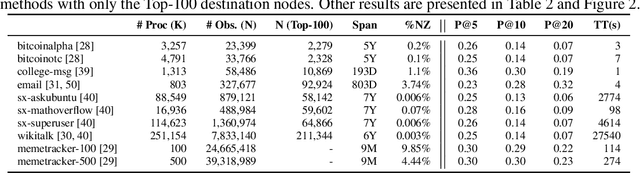
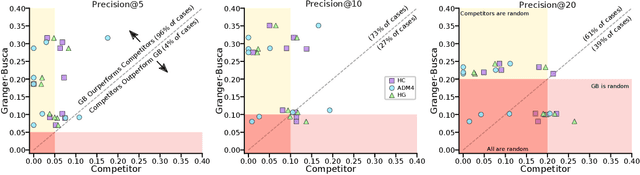
We here focus on the task of learning Granger causality matrices for multivariate point processes. In order to accomplish this task, our work is the first to explore the use of Wold processes. By doing so, we are able to develop asymptotically fast MCMC learning algorithms. With $N$ being the total number of events and $K$ the number of processes, our learning algorithm has a $O(N(\,\log(N)\,+\,\log(K)))$ cost per iteration. This is much faster than the $O(N^3\,K^2)$ or $O(K^3)$ for the state of the art. Our approach, called GrangerBusca, is validated on nine datasets from the Snap repository. This is an advance in relation to most prior efforts which focus mostly on subsets of the Memetracker dataset. Regarding accuracy, GrangerBusca is three times more accurate (in Precision@10) than the state of the art for the commonly explored subsets of the Memetracker data. Due to GrangerBusca's much lower training complexity, our approach is the only one able to train models for larger, full, sets of data.

A latent shared-component generative model for real-time disease surveillance using Twitter data

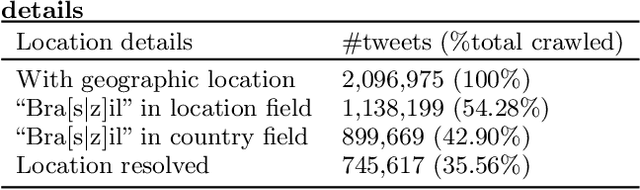
Exploiting the large amount of available data for addressing relevant social problems has been one of the key challenges in data mining. Such efforts have been recently named "data science for social good" and attracted the attention of several researchers and institutions. We give a contribution in this objective in this paper considering a difficult public health problem, the timely monitoring of dengue epidemics in small geographical areas. We develop a generative simple yet effective model to connect the fluctuations of disease cases and disease-related Twitter posts. We considered a hidden Markov process driving both, the fluctuations in dengue reported cases and the tweets issued in each region. We add a stable but random source of tweets to represent the posts when no disease cases are recorded. The model is learned through a Markov chain Monte Carlo algorithm that produces the posterior distribution of the relevant parameters. Using data from a significant number of large Brazilian towns, we demonstrate empirically that our model is able to predict well the next weeks of the disease counts using the tweets and disease cases jointly.