When can isotropy help adapt LLMs' next word prediction to numerical domains?

Recent studies have shown that vector representations of contextual embeddings learned by pre-trained large language models (LLMs) are effective in various downstream tasks in numerical domains. Despite their significant benefits, the tendency of LLMs to hallucinate in such domains can have severe consequences in applications such as energy, nature, finance, healthcare, retail and transportation, among others. To guarantee prediction reliability and accuracy in numerical domains, it is necessary to open the black-box and provide performance guarantees through explanation. However, there is little theoretical understanding of when pre-trained language models help solve numeric downstream tasks. This paper seeks to bridge this gap by understanding when the next-word prediction capability of LLMs can be adapted to numerical domains through a novel analysis based on the concept of isotropy in the contextual embedding space. Specifically, we consider a log-linear model for LLMs in which numeric data can be predicted from its context through a network with softmax in the output layer of LLMs (i.e., language model head in self-attention). We demonstrate that, in order to achieve state-of-the-art performance in numerical domains, the hidden representations of the LLM embeddings must possess a structure that accounts for the shift-invariance of the softmax function. By formulating a gradient structure of self-attention in pre-trained models, we show how the isotropic property of LLM embeddings in contextual embedding space preserves the underlying structure of representations, thereby resolving the shift-invariance problem and providing a performance guarantee. Experiments show that different characteristics of numeric data and model architecture could have different impacts on isotropy.

World Model-Based Learning for Long-Term Age of Information Minimization in Vehicular Networks

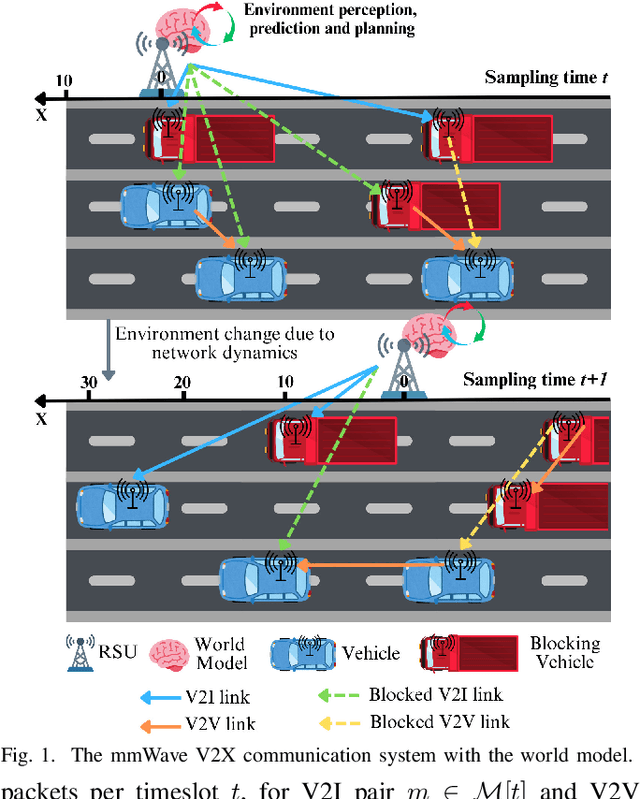
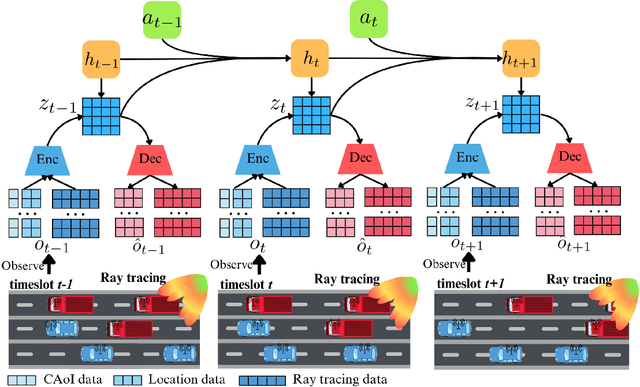
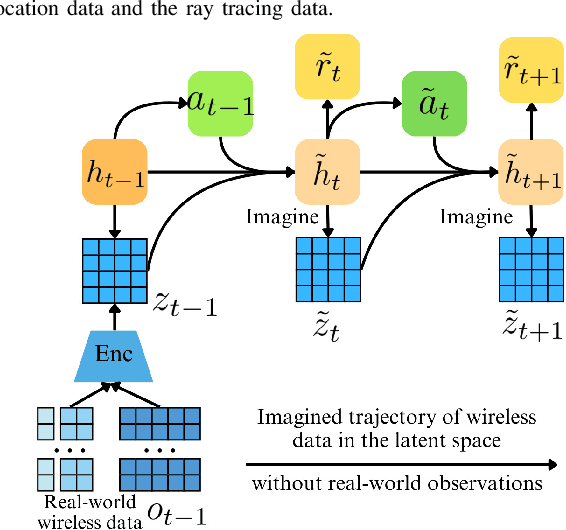
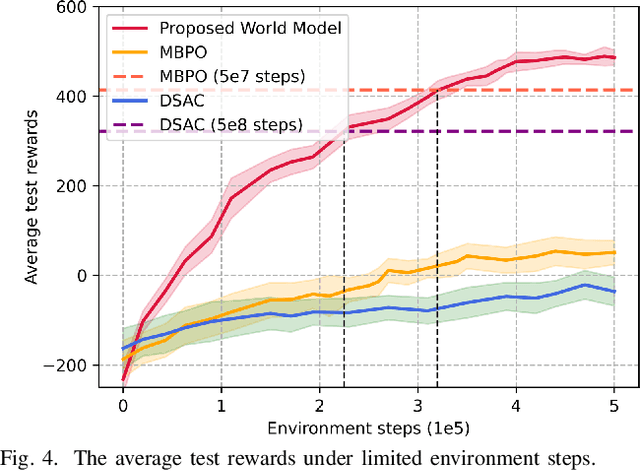
Traditional reinforcement learning (RL)-based learning approaches for wireless networks rely on expensive trial-and-error mechanisms and real-time feedback based on extensive environment interactions, which leads to low data efficiency and short-sighted policies. These limitations become particularly problematic in complex, dynamic networks with high uncertainty and long-term planning requirements. To address these limitations, in this paper, a novel world model-based learning framework is proposed to minimize packet-completeness-aware age of information (CAoI) in a vehicular network. Particularly, a challenging representative scenario is considered pertaining to a millimeter-wave (mmWave) vehicle-to-everything (V2X) communication network, which is characterized by high mobility, frequent signal blockages, and extremely short coherence time. Then, a world model framework is proposed to jointly learn a dynamic model of the mmWave V2X environment and use it to imagine trajectories for learning how to perform link scheduling. In particular, the long-term policy is learned in differentiable imagined trajectories instead of environment interactions. Moreover, owing to its imagination abilities, the world model can jointly predict time-varying wireless data and optimize link scheduling in real-world wireless and V2X networks. Thus, during intervals without actual observations, the world model remains capable of making efficient decisions. Extensive experiments are performed on a realistic simulator based on Sionna that integrates physics-based end-to-end channel modeling, ray-tracing, and scene geometries with material properties. Simulation results show that the proposed world model achieves a significant improvement in data efficiency, and achieves 26% improvement and 16% improvement in CAoI, respectively, compared to the model-based RL (MBRL) method and the model-free RL (MFRL) method.

DMWM: Dual-Mind World Model with Long-Term Imagination

Imagination in world models is crucial for enabling agents to learn long-horizon policy in a sample-efficient manner. Existing recurrent state-space model (RSSM)-based world models depend on single-step statistical inference to capture the environment dynamics, and, hence, they are unable to perform long-term imagination tasks due to the accumulation of prediction errors. Inspired by the dual-process theory of human cognition, we propose a novel dual-mind world model (DMWM) framework that integrates logical reasoning to enable imagination with logical consistency. DMWM is composed of two components: an RSSM-based System 1 (RSSM-S1) component that handles state transitions in an intuitive manner and a logic-integrated neural network-based System 2 (LINN-S2) component that guides the imagination process through hierarchical deep logical reasoning. The inter-system feedback mechanism is designed to ensure that the imagination process follows the logical rules of the real environment. The proposed framework is evaluated on benchmark tasks that require long-term planning from the DMControl suite. Extensive experimental results demonstrate that the proposed framework yields significant improvements in terms of logical coherence, trial efficiency, data efficiency and long-term imagination over the state-of-the-art world models.

A Fast Graph Kernel Based Classification Method for Wireless Link Scheduling on Riemannian Manifold

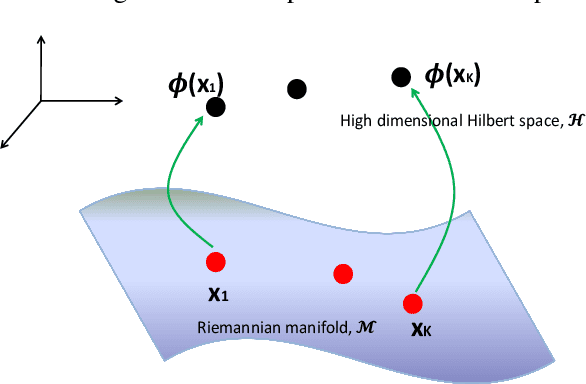
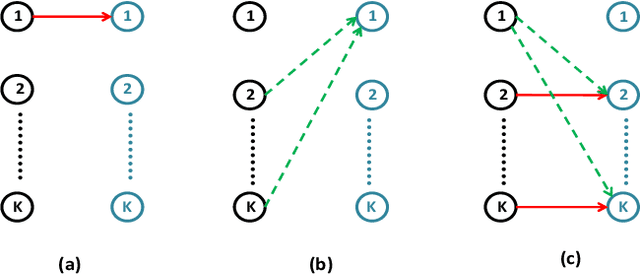
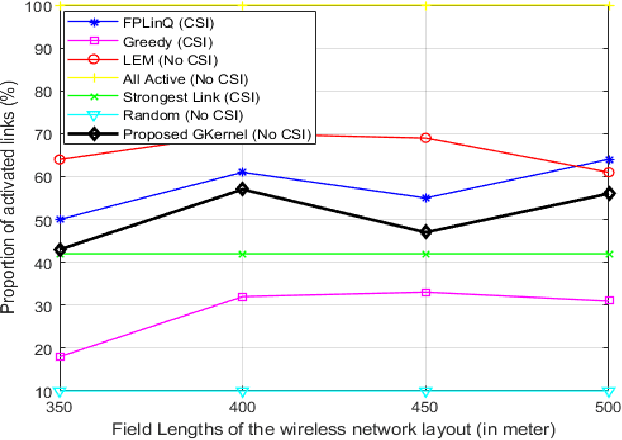
In this paper, we propose a novel graph kernel method for the wireless link scheduling problem in device-to-device (D2D) networks on Riemannian manifold. The link scheduling problem can be considered as a binary classification problem since each D2D pair can only hold the state active or inactive. Our goal is to learn a novel metric that facilitates the design of an efficient but less computationally demanding machine learning (ML) solution for the binary classification task of link scheduling problem that requires no channel state information (CSI) and a fewer number of training samples as opposed to other benchmark ML algorithms. To this aim, we first represent the wireless D2D network as a graph and model the features of each D2D pair, including its communication and interference links, as regularized (i.e., positively-shifted) Laplacian matrices which are symmetric positive definite (SPD) one. By doing so, we represent the feature information of each D2D pair as a point on the SPD manifold, and we analyze the topology through Riemannian geometry. We compute the Riemannian metric, e.g., Log-Euclidean metric (LEM), which are suitable distance measures between the regularized Laplacian matrices. The LEM is then utilized to define a positive definite graph kernel for the binary classification of the link scheduling decisions. Simulation results demonstrate that the proposed graph Kernel-based method is computationally less demanding and achieves a sum rate of more than 95% of benchmark algorithm FPLinQ [1] for 10 D2D pairs without using CSI and less than a hundred training network layouts.