Geometric Machine Learning for Channel Covariance Estimation in Vehicular Networks

Learning the covariance matrices of spatially-correlated wireless channels, in millimeter-wave (mmWave) vehicular communication, can be utilized in designing environmen-taware beamforming codebooks. Such channel covariance matrices can be represented on non-Euclidean Riemannian manifolds, thanks to their symmetric positive definite (SPD) characteristics. Consequently in this paper, we propose a Riemannian-Geometric machine learning (G-ML) approach for estimating the channel covariance matrices based on unsupervised K-Means model. The proposed K-means algorithm utilizes Log-Euclidean metric (LEM) as the distance measure among channel covariance matrices over the Riemannian manifolds. We show that our proposed K-Means G-ML model can achieve up to 80% less error compared to Euclidean-based K-Means algorithm, which applies clustering on the channel vectors themselves.

A Fast Graph Kernel Based Classification Method for Wireless Link Scheduling on Riemannian Manifold

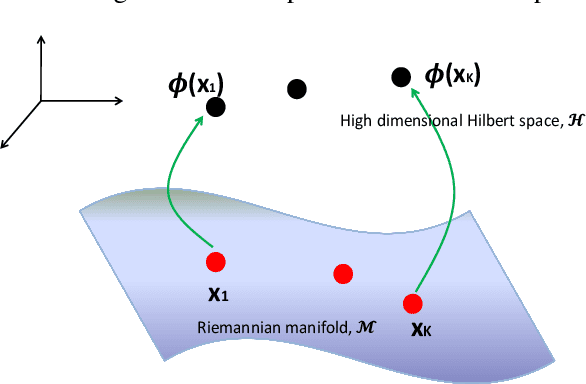
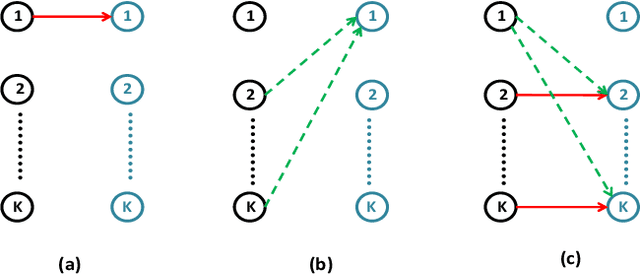
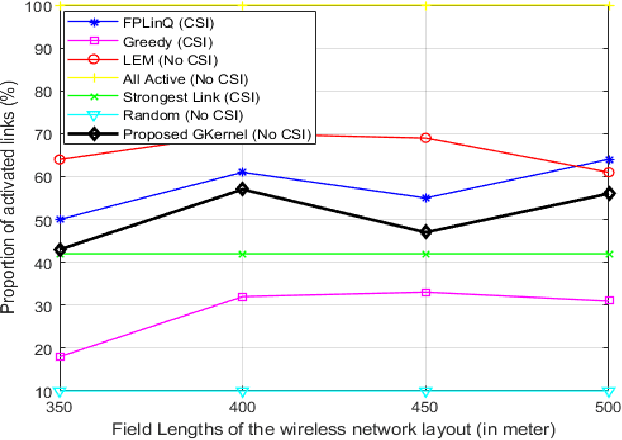
In this paper, we propose a novel graph kernel method for the wireless link scheduling problem in device-to-device (D2D) networks on Riemannian manifold. The link scheduling problem can be considered as a binary classification problem since each D2D pair can only hold the state active or inactive. Our goal is to learn a novel metric that facilitates the design of an efficient but less computationally demanding machine learning (ML) solution for the binary classification task of link scheduling problem that requires no channel state information (CSI) and a fewer number of training samples as opposed to other benchmark ML algorithms. To this aim, we first represent the wireless D2D network as a graph and model the features of each D2D pair, including its communication and interference links, as regularized (i.e., positively-shifted) Laplacian matrices which are symmetric positive definite (SPD) one. By doing so, we represent the feature information of each D2D pair as a point on the SPD manifold, and we analyze the topology through Riemannian geometry. We compute the Riemannian metric, e.g., Log-Euclidean metric (LEM), which are suitable distance measures between the regularized Laplacian matrices. The LEM is then utilized to define a positive definite graph kernel for the binary classification of the link scheduling decisions. Simulation results demonstrate that the proposed graph Kernel-based method is computationally less demanding and achieves a sum rate of more than 95% of benchmark algorithm FPLinQ [1] for 10 D2D pairs without using CSI and less than a hundred training network layouts.

Wireless Link Scheduling via Interference-aware Symmetric Positive Definite Connectivity Manifolds

In this paper, we investigate the fundamental problem of wireless link scheduling in device-to-device (D2D) networks, through the lens of Riemannian geometry. Our goal is to find a novel metric to characterize interference among D2D pairs, which can pave the way towards efficient and fast scheduling algorithms. Towards achieving this goal, we first model the connectivity pattern of each D2D pair, including its interference links, as a positively-shifted Laplacian matrix, which is a symmetric positive definite (SPD) one. Noting that SPD matrices constitute a non-Euclidean manifold, we represent each of the D2D pairs as a point on the SPD (i.e., conic) manifold, which is analyzed via Riemannian geometry. Accordingly we employ Riemannian metrics (e.g., Log-Euclidean metric "LEM"), which are suitable measures of distances on manifolds, to characterize the interference among D2D points on the SPD manifold. To validate the effectiveness of the proposed LEM-based interference measure, we propose a sequential link selection algorithm that schedules D2D pairs in a descending order of their signal-to-noise ratio (SNR), while keeping their LEM distances towards the already-scheduled pairs on the Riemannian manifold to be greater than a certain LEM threshold. Such LEM-based condition is equivalent to limiting the interference from potential D2D pairs to be below certain threshold. We show that the proposed LEM-based scheduling algorithm achieves sum rate of more than 86% of state-of-the-art ones (e.g., FPLinQ), while only requiring spatial locations of D2D pairs, as opposed to requiring full channel state information (CSI).