On the interaction between Autonomous Mobility-on-Demand systems and the power network: models and coordination algorithms

We study the interaction between a fleet of electric, self-driving vehicles servicing on-demand transportation requests (referred to as Autonomous Mobility-on-Demand, or AMoD, system) and the electric power network. We propose a model that captures the coupling between the two systems stemming from the vehicles' charging requirements and captures time-varying customer demand and power generation costs, road congestion, battery depreciation, and power transmission and distribution constraints. We then leverage the model to jointly optimize the operation of both systems. We devise an algorithmic procedure to losslessly reduce the problem size by bundling customer requests, allowing it to be efficiently solved by off-the-shelf linear programming solvers. Next, we show that the socially optimal solution to the joint problem can be enforced as a general equilibrium, and we provide a dual decomposition algorithm that allows self-interested agents to compute the market clearing prices without sharing private information. We assess the performance of the mode by studying a hypothetical AMoD system in Dallas-Fort Worth and its impact on the Texas power network. Lack of coordination between the AMoD system and the power network can cause a 4.4% increase in the price of electricity in Dallas-Fort Worth; conversely, coordination between the AMoD system and the power network could reduce electricity expenditure compared to the case where no cars are present (despite the increased demand for electricity) and yield savings of up $147M/year. Finally, we provide a receding-horizon implementation and assess its performance with agent-based simulations. Collectively, the results of this paper provide a first-of-a-kind characterization of the interaction between electric-powered AMoD systems and the power network, and shed additional light on the economic and societal value of AMoD.

Data-Driven Model Predictive Control of Autonomous Mobility-on-Demand Systems

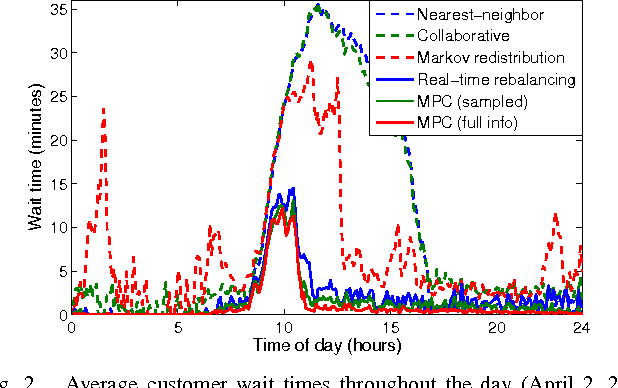
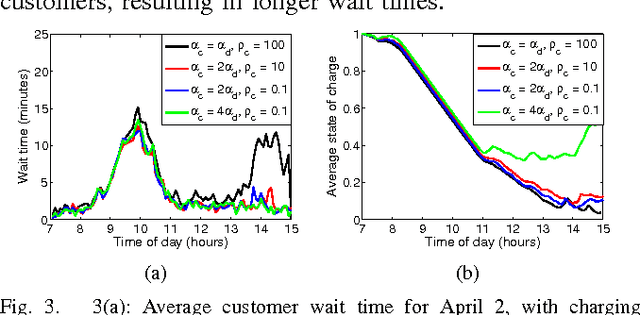
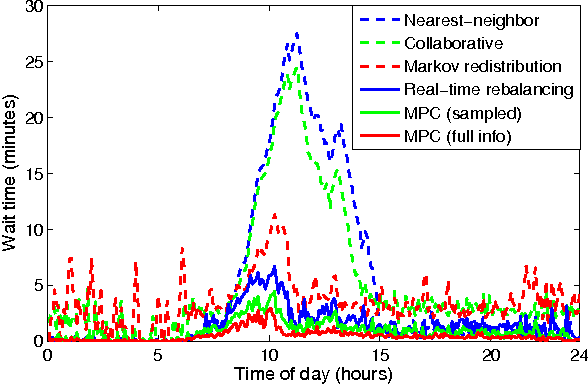
The goal of this paper is to present an end-to-end, data-driven framework to control Autonomous Mobility-on-Demand systems (AMoD, i.e. fleets of self-driving vehicles). We first model the AMoD system using a time-expanded network, and present a formulation that computes the optimal rebalancing strategy (i.e., preemptive repositioning) and the minimum feasible fleet size for a given travel demand. Then, we adapt this formulation to devise a Model Predictive Control (MPC) algorithm that leverages short-term demand forecasts based on historical data to compute rebalancing strategies. We test the end-to-end performance of this controller with a state-of-the-art LSTM neural network to predict customer demand and real customer data from DiDi Chuxing: we show that this approach scales very well for large systems (indeed, the computational complexity of the MPC algorithm does not depend on the number of customers and of vehicles in the system) and outperforms state-of-the-art rebalancing strategies by reducing the mean customer wait time by up to to 89.6%.