Generative AI for Brane Configurations, Tropical Coamoeba and 4d N=1 Quiver Gauge Theories

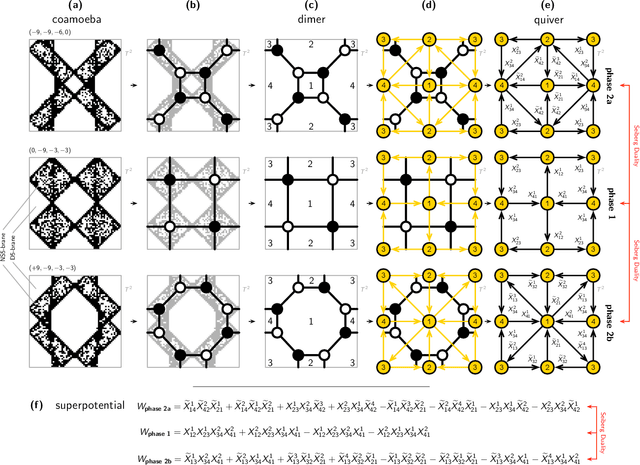
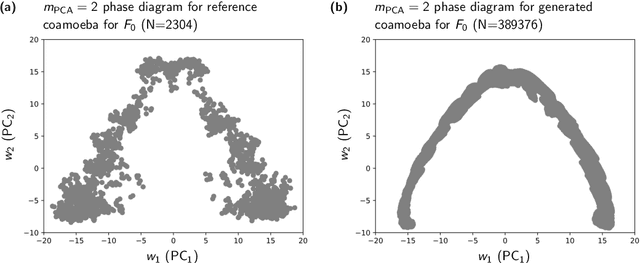
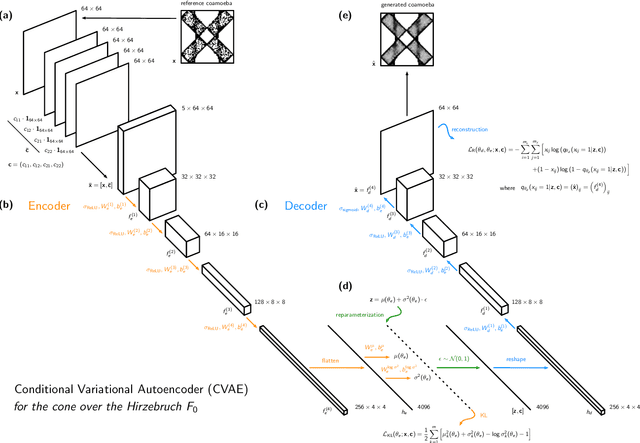
We introduce a generative AI model to obtain Type IIB brane configurations that realize toric phases of a family of 4d N=1 supersymmetric gauge theories. These 4d N=1 quiver gauge theories are worldvolume theories of a D3-brane probing a toric Calabi-Yau 3-fold. The Type IIB brane configurations that realize this family of 4d N=1 theories are known as brane tilings and are given by the tropical coamoeba projection of the mirror curve associated with the toric Calabi-Yau 3-fold. The shape of the mirror curve and its coamoeba projection, as well as the corresponding Type IIB brane configuration and the toric phase of the 4d N=1 theory, all depend on the complex structure moduli parameterizing the mirror curve. We train a generative AI model, a conditional variational autoencoder (CVAE), that takes a choice of complex structure moduli as input and generates the corresponding tropical coamoeba. This enables us not only to obtain a high-resolution representation of the entire phase space for a family of brane tilings corresponding to the same toric Calabi-Yau 3-fold, but also to continuously track the movements of the mirror curve and individual branes in the corresponding Type IIB brane configurations during phase transitions associated with Seiberg duality.

Learning BPS Spectra and the Gap Conjecture

We explore statistical properties of BPS q-series for 3d N=2 strongly coupled supersymmetric theories that correspond to a particular family of 3-manifolds Y. We discover that gaps between exponents in the q-series are statistically more significant at the beginning of the q-series compared to gaps that appear in higher powers of q. Our observations are obtained by calculating saliencies of q-series features used as input data for principal component analysis, which is a standard example of an explainable machine learning technique that allows for a direct calculation and a better analysis of feature saliencies.

Machine Learning Regularization for the Minimum Volume Formula of Toric Calabi-Yau 3-folds

We present a collection of explicit formulas for the minimum volume of Sasaki-Einstein 5-manifolds. The cone over these 5-manifolds is a toric Calabi-Yau 3-fold. These toric Calabi-Yau 3-folds are associated with an infinite class of 4d N=1 supersymmetric gauge theories, which are realized as worldvolume theories of D3-branes probing the toric Calabi-Yau 3-folds. Under the AdS/CFT correspondence, the minimum volume of the Sasaki-Einstein base is inversely proportional to the central charge of the corresponding 4d N=1 superconformal field theories. The presented formulas for the minimum volume are in terms of geometric invariants of the toric Calabi-Yau 3-folds. These explicit results are derived by implementing machine learning regularization techniques that advance beyond previous applications of machine learning for determining the minimum volume. Moreover, the use of machine learning regularization allows us to present interpretable and explainable formulas for the minimum volume. Our work confirms that, even for extensive sets of toric Calabi-Yau 3-folds, the proposed formulas approximate the minimum volume with remarkable accuracy.

Unsupervised Machine Learning Techniques for Exploring Tropical Coamoeba, Brane Tilings and Seiberg Duality

We introduce unsupervised machine learning techniques in order to identify toric phases of 4d N=1 supersymmetric gauge theories corresponding to the same toric Calabi-Yau 3-fold. These 4d N=1 supersymmetric gauge theories are worldvolume theories of a D3-brane probing a toric Calabi-Yau 3-fold and are realized in terms of a Type IIB brane configuration known as a brane tiling. It corresponds to the skeleton graph of the coamoeba projection of the mirror curve associated to the toric Calabi-Yau 3-fold. When we vary the complex structure moduli of the mirror Calabi-Yau 3-fold, the coamoeba and the corresponding brane tilings change their shape, giving rise to different toric phases related by Seiberg duality. We illustrate that by employing techniques such as principal component analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE), we can project the space of coamoeba labelled by complex structure moduli down to a lower dimensional phase space with phase boundaries corresponding to Seiberg duality. In this work, we illustrate this technique by obtaining a 2-dimensional phase diagram for brane tilings corresponding to the cone over the zeroth Hirzebruch surface F0.