What makes math problems hard for reinforcement learning: a case study

Using a long-standing conjecture from combinatorial group theory, we explore, from multiple angles, the challenges of finding rare instances carrying disproportionately high rewards. Based on lessons learned in the mathematical context defined by the Andrews-Curtis conjecture, we propose algorithmic improvements that can be relevant in other domains with ultra-sparse reward problems. Although our case study can be formulated as a game, its shortest winning sequences are potentially $10^6$ or $10^9$ times longer than those encountered in chess. In the process of our study, we demonstrate that one of the potential counterexamples due to Akbulut and Kirby, whose status escaped direct mathematical methods for 39 years, is stably AC-trivial.

Learning BPS Spectra and the Gap Conjecture

We explore statistical properties of BPS q-series for 3d N=2 strongly coupled supersymmetric theories that correspond to a particular family of 3-manifolds Y. We discover that gaps between exponents in the q-series are statistically more significant at the beginning of the q-series compared to gaps that appear in higher powers of q. Our observations are obtained by calculating saliencies of q-series features used as input data for principal component analysis, which is a standard example of an explainable machine learning technique that allows for a direct calculation and a better analysis of feature saliencies.

Rigor with Machine Learning from Field Theory to the Poincaré Conjecture

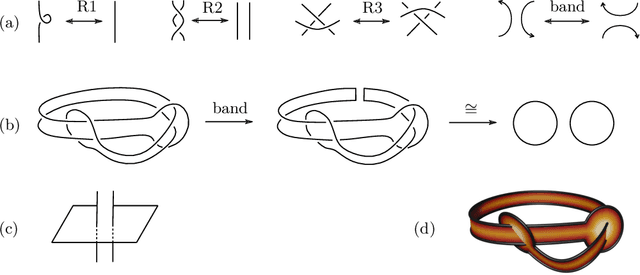
Machine learning techniques are increasingly powerful, leading to many breakthroughs in the natural sciences, but they are often stochastic, error-prone, and blackbox. How, then, should they be utilized in fields such as theoretical physics and pure mathematics that place a premium on rigor and understanding? In this Perspective we discuss techniques for obtaining rigor in the natural sciences with machine learning. Non-rigorous methods may lead to rigorous results via conjecture generation or verification by reinforcement learning. We survey applications of these techniques-for-rigor ranging from string theory to the smooth $4$d Poincar\'e conjecture in low-dimensional topology. One can also imagine building direct bridges between machine learning theory and either mathematics or theoretical physics. As examples, we describe a new approach to field theory motivated by neural network theory, and a theory of Riemannian metric flows induced by neural network gradient descent, which encompasses Perelman's formulation of the Ricci flow that was utilized to resolve the $3$d Poincar\'e conjecture.

Searching for ribbons with machine learning

We apply Bayesian optimization and reinforcement learning to a problem in topology: the question of when a knot bounds a ribbon disk. This question is relevant in an approach to disproving the four-dimensional smooth Poincar\'e conjecture; using our programs, we rule out many potential counterexamples to the conjecture. We also show that the programs are successful in detecting many ribbon knots in the range of up to 70 crossings.

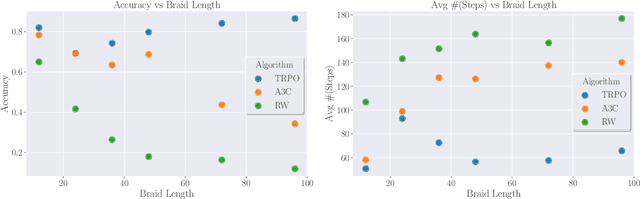
Learning to Unknot

We introduce natural language processing into the study of knot theory, as made natural by the braid word representation of knots. We study the UNKNOT problem of determining whether or not a given knot is the unknot. After describing an algorithm to randomly generate $N$-crossing braids and their knot closures and discussing the induced prior on the distribution of knots, we apply binary classification to the UNKNOT decision problem. We find that the Reformer and shared-QK Transformer network architectures outperform fully-connected networks, though all perform well. Perhaps surprisingly, we find that accuracy increases with the length of the braid word, and that the networks learn a direct correlation between the confidence of their predictions and the degree of the Jones polynomial. Finally, we utilize reinforcement learning (RL) to find sequences of Markov moves and braid relations that simplify knots and can identify unknots by explicitly giving the sequence of unknotting actions. Trust region policy optimization (TRPO) performs consistently well for a wide range of crossing numbers and thoroughly outperformed other RL algorithms and random walkers. Studying these actions, we find that braid relations are more useful in simplifying to the unknot than one of the Markov moves.