Rigor with Machine Learning from Field Theory to the Poincaré Conjecture
Paper and Code
Feb 20, 2024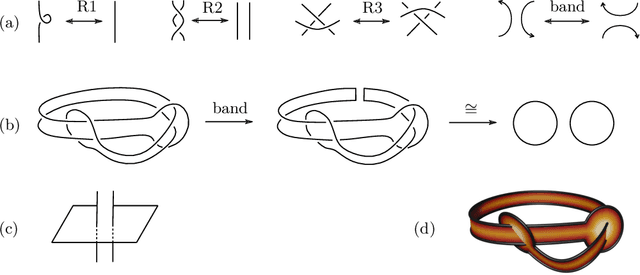
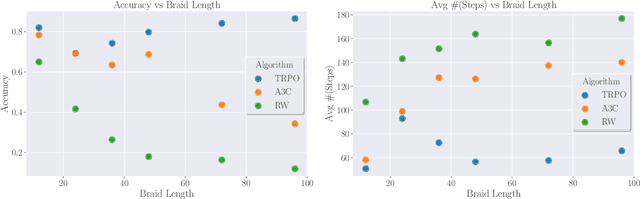
Machine learning techniques are increasingly powerful, leading to many breakthroughs in the natural sciences, but they are often stochastic, error-prone, and blackbox. How, then, should they be utilized in fields such as theoretical physics and pure mathematics that place a premium on rigor and understanding? In this Perspective we discuss techniques for obtaining rigor in the natural sciences with machine learning. Non-rigorous methods may lead to rigorous results via conjecture generation or verification by reinforcement learning. We survey applications of these techniques-for-rigor ranging from string theory to the smooth $4$d Poincar\'e conjecture in low-dimensional topology. One can also imagine building direct bridges between machine learning theory and either mathematics or theoretical physics. As examples, we describe a new approach to field theory motivated by neural network theory, and a theory of Riemannian metric flows induced by neural network gradient descent, which encompasses Perelman's formulation of the Ricci flow that was utilized to resolve the $3$d Poincar\'e conjecture.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge