LISR: Learning Linear 3D Implicit Surface Representation Using Compactly Supported Radial Basis Functions

Implicit 3D surface reconstruction of an object from its partial and noisy 3D point cloud scan is the classical geometry processing and 3D computer vision problem. In the literature, various 3D shape representations have been developed, differing in memory efficiency and shape retrieval effectiveness, such as volumetric, parametric, and implicit surfaces. Radial basis functions provide memory-efficient parameterization of the implicit surface. However, we show that training a neural network using the mean squared error between the ground-truth implicit surface and the linear basis-based implicit surfaces does not converge to the global solution. In this work, we propose locally supported compact radial basis functions for a linear representation of the implicit surface. This representation enables us to generate 3D shapes with arbitrary topologies at any resolution due to their continuous nature. We then propose a neural network architecture for learning the linear implicit shape representation of the 3D surface of an object. We learn linear implicit shapes within a supervised learning framework using ground truth Signed-Distance Field (SDF) data for guidance. The classical strategies face difficulties in finding linear implicit shapes from a given 3D point cloud due to numerical issues (requires solving inverse of a large matrix) in basis and query point selection. The proposed approach achieves better Chamfer distance and comparable F-score than the state-of-the-art approach on the benchmark dataset. We also show the effectiveness of the proposed approach by using it for the 3D shape completion task.

Learning Vision-based Robotic Manipulation Tasks Sequentially in Offline Reinforcement Learning Settings

With the rise of deep reinforcement learning (RL) methods, many complex robotic manipulation tasks are being solved. However, harnessing the full power of deep learning requires large datasets. Online-RL does not suit itself readily into this paradigm due to costly and time-taking agent environment interaction. Therefore recently, many offline-RL algorithms have been proposed to learn robotic tasks. But mainly, all such methods focus on a single task or multi-task learning, which requires retraining every time we need to learn a new task. Continuously learning tasks without forgetting previous knowledge combined with the power of offline deep-RL would allow us to scale the number of tasks by keep adding them one-after-another. In this paper, we investigate the effectiveness of regularisation-based methods like synaptic intelligence for sequentially learning image-based robotic manipulation tasks in an offline-RL setup. We evaluate the performance of this combined framework against common challenges of sequential learning: catastrophic forgetting and forward knowledge transfer. We performed experiments with different task combinations to analyze the effect of task ordering. We also investigated the effect of the number of object configurations and density of robot trajectories. We found that learning tasks sequentially helps in the propagation of knowledge from previous tasks, thereby reducing the time required to learn a new task. Regularisation based approaches for continuous learning like the synaptic intelligence method although helps in mitigating catastrophic forgetting but has shown only limited transfer of knowledge from previous tasks.

Robust Estimation of Reflection Symmetry in Noisy and Partial 3D Point Clouds

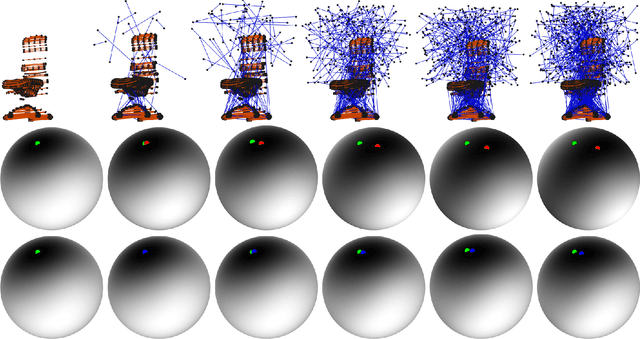
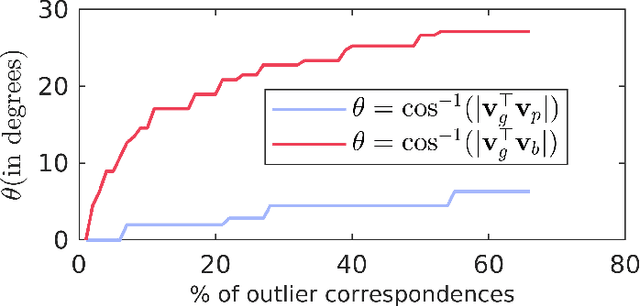
Detecting the reflection symmetry plane of an object represented by a 3D point cloud is a fundamental problem in 3D computer vision and geometry processing due to its various applications such as compression, object detection, robotic grasping, 3D surface reconstruction, etc. There exist several efficient approaches for solving this problem for clean 3D point clouds. However, this problem becomes difficult to solve in the presence of outliers and missing parts due to occlusions while scanning the objects through 3D scanners. The existing methods try to overcome these challenges mostly by voting-based techniques but fail in challenging settings. In this work, we propose a statistical estimator for the plane of reflection symmetry that is robust to outliers and missing parts. We pose the problem of finding the optimal estimator as an optimization problem on a 2-sphere that quickly converges to the global solution. We further propose a 3D point descriptor that is invariant to 3D reflection symmetry using the spectral properties of the geodesic distance matrix constructed from the neighbors of a point. This helps us in decoupling the chicken-and-egg problem of finding optimal symmetry plane and correspondences between the reflective symmetric points. We show that the proposed approach achieves the state-of-the-art performance on the benchmarks dataset.

RGL-NET: A Recurrent Graph Learning framework for Progressive Part Assembly

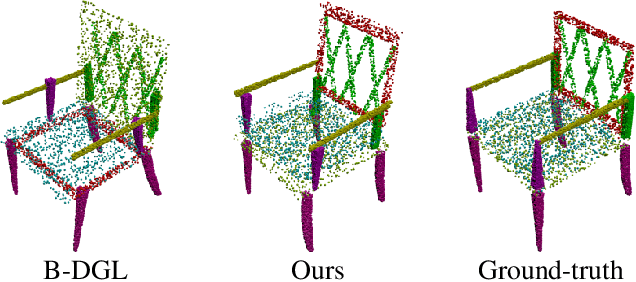
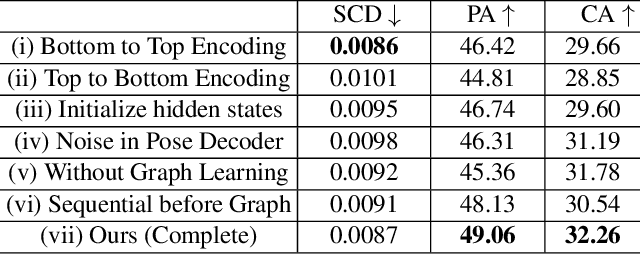
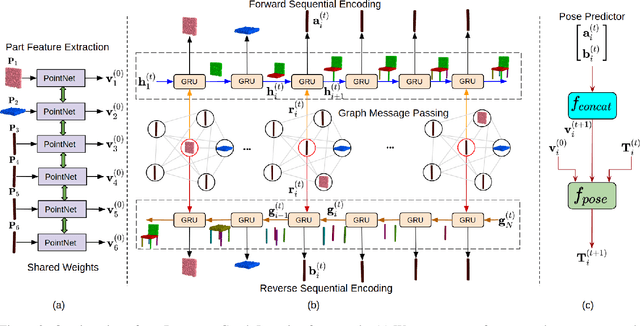
Autonomous assembly of objects is an essential task in robotics and 3D computer vision. It has been studied extensively in robotics as a problem of motion planning, actuator control and obstacle avoidance. However, the task of developing a generalized framework for assembly robust to structural variants remains relatively unexplored. In this work, we tackle this problem using a recurrent graph learning framework considering inter-part relations and the progressive update of the part pose. Our network can learn more plausible predictions of shape structure by accounting for priorly assembled parts. Compared to the current state-of-the-art, our network yields up to 10% improvement in part accuracy and up to 15% improvement in connectivity accuracy on the PartNet dataset. Moreover, our resulting latent space facilitates exciting applications such as shape recovery from the point-cloud components. We conduct extensive experiments to justify our design choices and demonstrate the effectiveness of the proposed framework.

Fast and Accurate Intrinsic Symmetry Detection

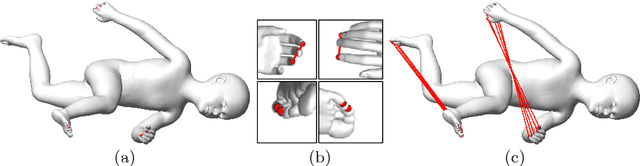
In computer vision and graphics, various types of symmetries are extensively studied since symmetry present in objects is a fundamental cue for understanding the shape and the structure of objects. In this work, we detect the intrinsic reflective symmetry in triangle meshes where we have to find the intrinsically symmetric point for each point of the shape. We establish correspondences between functions defined on the shapes by extending the functional map framework and then recover the point-to-point correspondences. Previous approaches using the functional map for this task find the functional correspondences matrix by solving a non-linear optimization problem which makes them slow. In this work, we propose a closed form solution for this matrix which makes our approach faster. We find the closed-form solution based on our following results. If the given shape is intrinsically symmetric, then the shortest length geodesic between two intrinsically symmetric points is also intrinsically symmetric. If an eigenfunction of the Laplace-Beltrami operator for the given shape is an even (odd) function, then its restriction on the shortest length geodesic between two intrinsically symmetric points is also an even (odd) function. The sign of a low-frequency eigenfunction is the same on the neighboring points. Our method is invariant to the ordering of the eigenfunctions and has the least time complexity. We achieve the best performance on the SCAPE dataset and comparable performance with the state-of-the-art methods on the TOSCA dataset.

Detecting Approximate Reflection Symmetry in a Point Set using Optimization on Manifold

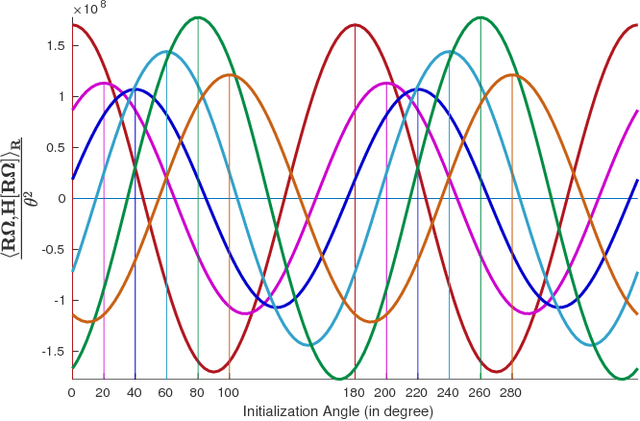
We propose an algorithm to detect approximate reflection symmetry present in a set of volumetrically distributed points belonging to $\mathbb{R}^d$ containing a distorted reflection symmetry pattern. We pose the problem of detecting approximate reflection symmetry as the problem of establishing the correspondences between the points which are reflections of each other and determining the reflection symmetry transformation. We formulate an optimization framework in which the problem of establishing the correspondences amounts to solving a linear assignment problem and the problem of determining the reflection symmetry transformation amounts to an optimization problem on a smooth Riemannian product manifold. The proposed approach estimates the symmetry from the distribution of the points and is descriptor independent. We evaluate the robustness of our approach by varying the amount of distortion in a perfect reflection symmetry pattern where we perturb each point by a different amount of perturbation. We demonstrate the effectiveness of the method by applying it to the problem of 2-D reflection symmetry detection along with relevant comparisons.

SymmSLIC: Symmetry Aware Superpixel Segmentation and its Applications

Over-segmentation of an image into superpixels has become a useful tool for solving various problems in image processing and computer vision. Reflection symmetry is quite prevalent in both natural and man-made objects and is an essential cue in understanding and grouping the objects in natural scenes. Existing algorithms for estimating superpixels do not preserve the reflection symmetry of an object which leads to different sizes and shapes of superpixels across the symmetry axis. In this work, we propose an algorithm to over-segment an image through the propagation of reflection symmetry evident at the pixel level to superpixel boundaries. In order to achieve this goal, we first find the reflection symmetry in the image and represent it by a set of pairs of pixels which are mirror reflections of each other. We partition the image into superpixels while preserving this reflection symmetry through an iterative algorithm. We compare the proposed method with state-of-the-art superpixel generation methods and show the effectiveness in preserving the size and shape of superpixel boundaries across the reflection symmetry axes. We also present two applications, symmetry axes detection and unsupervised symmetric object segmentation, to illustrate the effectiveness of the proposed approach.