Robust Estimation of Reflection Symmetry in Noisy and Partial 3D Point Clouds
Paper and Code
Sep 21, 2021
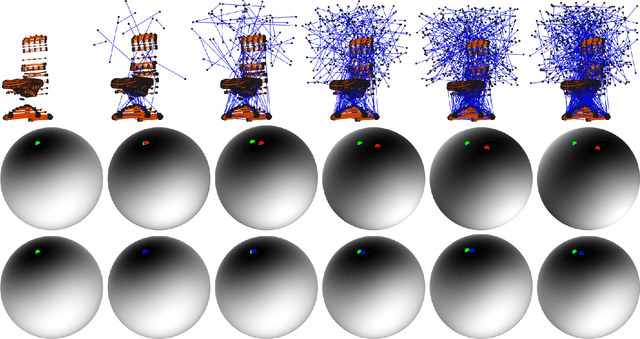
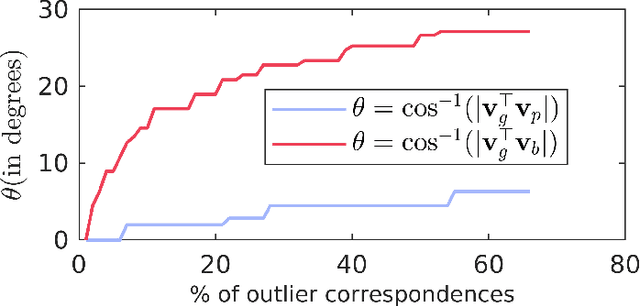

Detecting the reflection symmetry plane of an object represented by a 3D point cloud is a fundamental problem in 3D computer vision and geometry processing due to its various applications such as compression, object detection, robotic grasping, 3D surface reconstruction, etc. There exist several efficient approaches for solving this problem for clean 3D point clouds. However, this problem becomes difficult to solve in the presence of outliers and missing parts due to occlusions while scanning the objects through 3D scanners. The existing methods try to overcome these challenges mostly by voting-based techniques but fail in challenging settings. In this work, we propose a statistical estimator for the plane of reflection symmetry that is robust to outliers and missing parts. We pose the problem of finding the optimal estimator as an optimization problem on a 2-sphere that quickly converges to the global solution. We further propose a 3D point descriptor that is invariant to 3D reflection symmetry using the spectral properties of the geodesic distance matrix constructed from the neighbors of a point. This helps us in decoupling the chicken-and-egg problem of finding optimal symmetry plane and correspondences between the reflective symmetric points. We show that the proposed approach achieves the state-of-the-art performance on the benchmarks dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge