Fast and Accurate Intrinsic Symmetry Detection
Paper and Code
Oct 29, 2018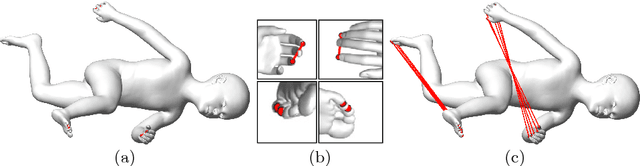

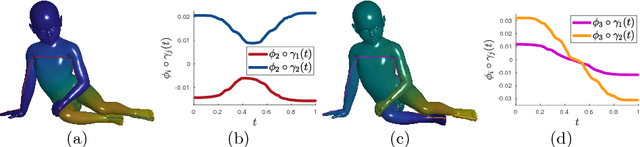

In computer vision and graphics, various types of symmetries are extensively studied since symmetry present in objects is a fundamental cue for understanding the shape and the structure of objects. In this work, we detect the intrinsic reflective symmetry in triangle meshes where we have to find the intrinsically symmetric point for each point of the shape. We establish correspondences between functions defined on the shapes by extending the functional map framework and then recover the point-to-point correspondences. Previous approaches using the functional map for this task find the functional correspondences matrix by solving a non-linear optimization problem which makes them slow. In this work, we propose a closed form solution for this matrix which makes our approach faster. We find the closed-form solution based on our following results. If the given shape is intrinsically symmetric, then the shortest length geodesic between two intrinsically symmetric points is also intrinsically symmetric. If an eigenfunction of the Laplace-Beltrami operator for the given shape is an even (odd) function, then its restriction on the shortest length geodesic between two intrinsically symmetric points is also an even (odd) function. The sign of a low-frequency eigenfunction is the same on the neighboring points. Our method is invariant to the ordering of the eigenfunctions and has the least time complexity. We achieve the best performance on the SCAPE dataset and comparable performance with the state-of-the-art methods on the TOSCA dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge