Factor Informed Double Deep Learning For Average Treatment Effect Estimation

We investigate the problem of estimating the average treatment effect (ATE) under a very general setup where the covariates can be high-dimensional, highly correlated, and can have sparse nonlinear effects on the propensity and outcome models. We present the use of a Double Deep Learning strategy for estimation, which involves combining recently developed factor-augmented deep learning-based estimators, FAST-NN, for both the response functions and propensity scores to achieve our goal. By using FAST-NN, our method can select variables that contribute to propensity and outcome models in a completely nonparametric and algorithmic manner and adaptively learn low-dimensional function structures through neural networks. Our proposed novel estimator, FIDDLE (Factor Informed Double Deep Learning Estimator), estimates ATE based on the framework of augmented inverse propensity weighting AIPW with the FAST-NN-based response and propensity estimates. FIDDLE consistently estimates ATE even under model misspecification and is flexible to also allow for low-dimensional covariates. Our method achieves semiparametric efficiency under a very flexible family of propensity and outcome models. We present extensive numerical studies on synthetic and real datasets to support our theoretical guarantees and establish the advantages of our methods over other traditional choices, especially when the data dimension is large.

Covariate-Balancing-Aware Interpretable Deep Learning models for Treatment Effect Estimation

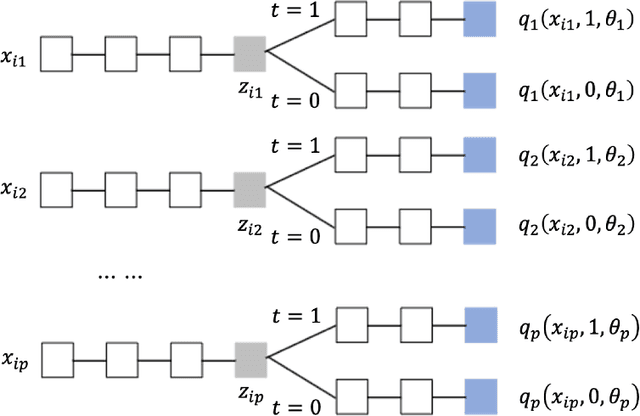
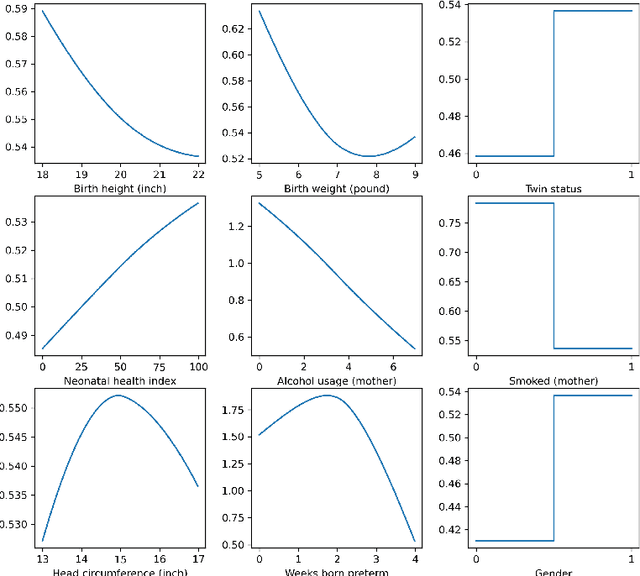
Estimating treatment effects is of great importance for many biomedical applications with observational data. Particularly, interpretability of the treatment effects is preferable for many biomedical researchers. In this paper, we first give a theoretical analysis and propose an upper bound for the bias of average treatment effect estimation under the strong ignorability assumption. The proposed upper bound consists of two parts: training error for factual outcomes, and the distance between treated and control distributions. We use the Weighted Energy Distance (WED) to measure the distance between two distributions. Motivated by the theoretical analysis, we implement this upper bound as an objective function being minimized by leveraging a novel additive neural network architecture, which combines the expressivity of deep neural network, the interpretability of generalized additive model, the sufficiency of the balancing score for estimation adjustment, and covariate balancing properties of treated and control distributions, for estimating average treatment effects from observational data. Furthermore, we impose a so-called weighted regularization procedure based on non-parametric theory, to obtain some desirable asymptotic properties. The proposed method is illustrated by re-examining the benchmark datasets for causal inference, and it outperforms the state-of-art.