Rethinking the Structure of Stochastic Gradients: Empirical and Statistical Evidence

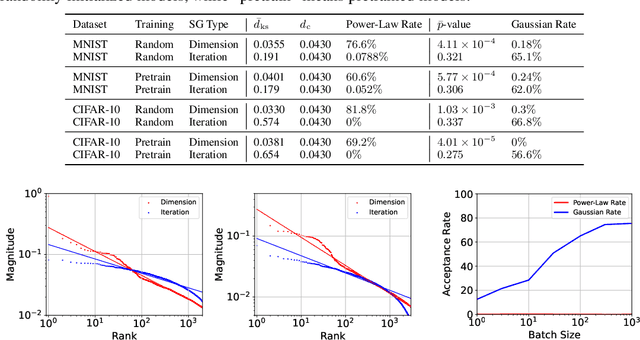
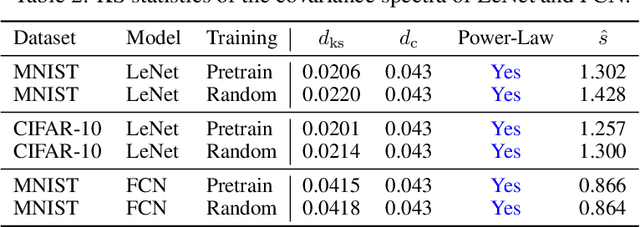
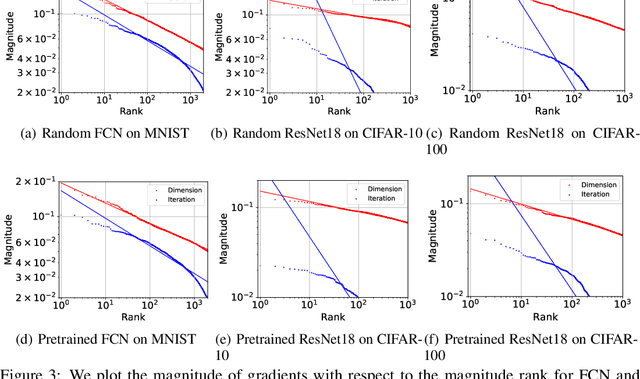
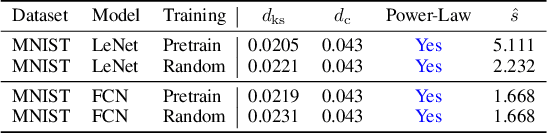
Stochastic gradients closely relate to both optimization and generalization of deep neural networks (DNNs). Some works attempted to explain the success of stochastic optimization for deep learning by the arguably heavy-tail properties of gradient noise, while other works presented theoretical and empirical evidence against the heavy-tail hypothesis on gradient noise. Unfortunately, formal statistical tests for analyzing the structure and heavy tails of stochastic gradients in deep learning are still under-explored. In this paper, we mainly make two contributions. First, we conduct formal statistical tests on the distribution of stochastic gradients and gradient noise across both parameters and iterations. Our statistical tests reveal that dimension-wise gradients usually exhibit power-law heavy tails, while iteration-wise gradients and stochastic gradient noise caused by minibatch training usually do not exhibit power-law heavy tails. Second, we further discover that the covariance spectra of stochastic gradients have the power-law structures in deep learning. While previous papers believed that the anisotropic structure of stochastic gradients matters to deep learning, they did not expect the gradient covariance can have such an elegant mathematical structure. Our work challenges the existing belief and provides novel insights on the structure of stochastic gradients in deep learning.

On the Power-Law Spectrum in Deep Learning: A Bridge to Protein Science

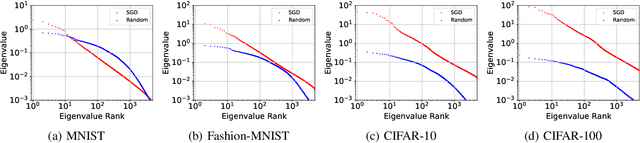
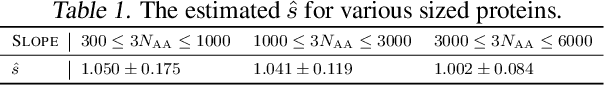
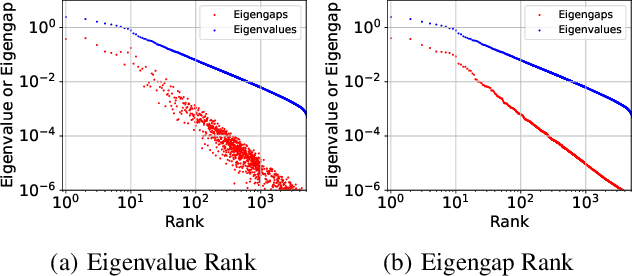
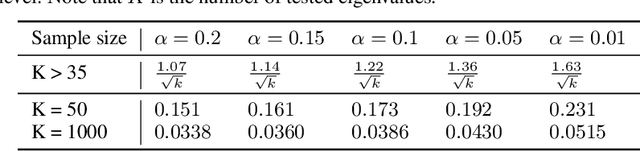
It is well-known that the Hessian matters to optimization, generalization, and even robustness of deep learning. Recent works empirically discovered that the Hessian spectrum in deep learning has a two-component structure that consists of a small number of large eigenvalues and a large number of nearly-zero eigenvalues. However, the theoretical mechanism behind the Hessian spectrum is still absent or under-explored. We are the first to theoretically and empirically demonstrate that the Hessian spectrums of well-trained deep neural networks exhibit simple power-law distributions. Our work further reveals how the power-law spectrum essentially matters to deep learning: (1) it leads to low-dimensional and robust learning space, and (2) it implicitly penalizes the variational free energy, which results in low-complexity solutions. We further used the power-law spectral framework as a powerful tool to demonstrate multiple novel behaviors of deep learning. Interestingly, the power-law spectrum is also known to be important in protein, which indicates a novel bridge between deep learning and protein science.