On the Power-Law Spectrum in Deep Learning: A Bridge to Protein Science

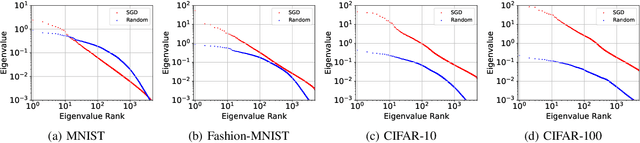
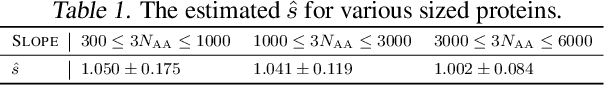
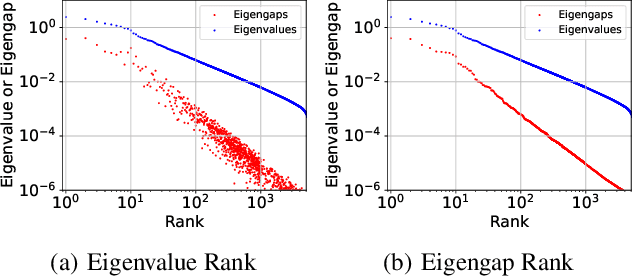
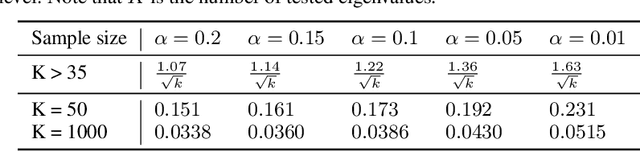
It is well-known that the Hessian matters to optimization, generalization, and even robustness of deep learning. Recent works empirically discovered that the Hessian spectrum in deep learning has a two-component structure that consists of a small number of large eigenvalues and a large number of nearly-zero eigenvalues. However, the theoretical mechanism behind the Hessian spectrum is still absent or under-explored. We are the first to theoretically and empirically demonstrate that the Hessian spectrums of well-trained deep neural networks exhibit simple power-law distributions. Our work further reveals how the power-law spectrum essentially matters to deep learning: (1) it leads to low-dimensional and robust learning space, and (2) it implicitly penalizes the variational free energy, which results in low-complexity solutions. We further used the power-law spectral framework as a powerful tool to demonstrate multiple novel behaviors of deep learning. Interestingly, the power-law spectrum is also known to be important in protein, which indicates a novel bridge between deep learning and protein science.