Qi Lyu
SeqWalker: Sequential-Horizon Vision-and-Language Navigation with Hierarchical Planning
Jan 08, 2026Abstract:Sequential-Horizon Vision-and-Language Navigation (SH-VLN) presents a challenging scenario where agents should sequentially execute multi-task navigation guided by complex, long-horizon language instructions. Current vision-and-language navigation models exhibit significant performance degradation with such multi-task instructions, as information overload impairs the agent's ability to attend to observationally relevant details. To address this problem, we propose SeqWalker, a navigation model built on a hierarchical planning framework. Our SeqWalker features: i) A High-Level Planner that dynamically selects global instructions into contextually relevant sub-instructions based on the agent's current visual observations, thus reducing cognitive load; ii) A Low-Level Planner incorporating an Exploration-Verification strategy that leverages the inherent logical structure of instructions for trajectory error correction. To evaluate SH-VLN performance, we also extend the IVLN dataset and establish a new benchmark. Extensive experiments are performed to demonstrate the superiority of the proposed SeqWalker.
CRISP: Contrastive Residual Injection and Semantic Prompting for Continual Video Instance Segmentation
Aug 14, 2025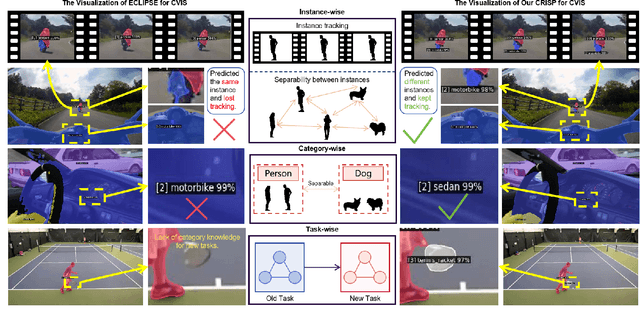
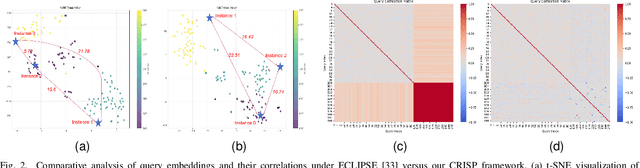
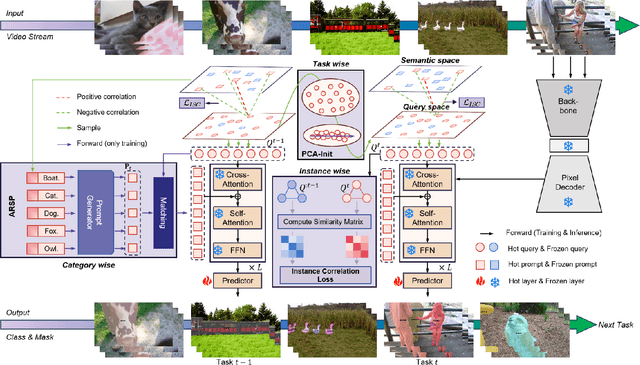
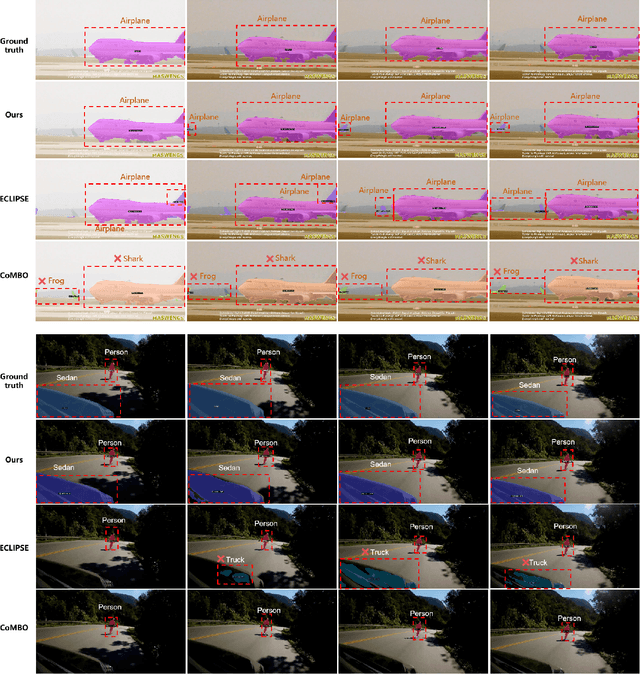
Abstract:Continual video instance segmentation demands both the plasticity to absorb new object categories and the stability to retain previously learned ones, all while preserving temporal consistency across frames. In this work, we introduce Contrastive Residual Injection and Semantic Prompting (CRISP), an earlier attempt tailored to address the instance-wise, category-wise, and task-wise confusion in continual video instance segmentation. For instance-wise learning, we model instance tracking and construct instance correlation loss, which emphasizes the correlation with the prior query space while strengthening the specificity of the current task query. For category-wise learning, we build an adaptive residual semantic prompt (ARSP) learning framework, which constructs a learnable semantic residual prompt pool generated by category text and uses an adjustive query-prompt matching mechanism to build a mapping relationship between the query of the current task and the semantic residual prompt. Meanwhile, a semantic consistency loss based on the contrastive learning is introduced to maintain semantic coherence between object queries and residual prompts during incremental training. For task-wise learning, to ensure the correlation at the inter-task level within the query space, we introduce a concise yet powerful initialization strategy for incremental prompts. Extensive experiments on YouTube-VIS-2019 and YouTube-VIS-2021 datasets demonstrate that CRISP significantly outperforms existing continual segmentation methods in the long-term continual video instance segmentation task, avoiding catastrophic forgetting and effectively improving segmentation and classification performance. The code is available at https://github.com/01upup10/CRISP.
Provable Subspace Identification Under Post-Nonlinear Mixtures
Oct 14, 2022

Abstract:Unsupervised mixture learning (UML) aims at identifying linearly or nonlinearly mixed latent components in a blind manner. UML is known to be challenging: Even learning linear mixtures requires highly nontrivial analytical tools, e.g., independent component analysis or nonnegative matrix factorization. In this work, the post-nonlinear (PNL) mixture model -- where unknown element-wise nonlinear functions are imposed onto a linear mixture -- is revisited. The PNL model is widely employed in different fields ranging from brain signal classification, speech separation, remote sensing, to causal discovery. To identify and remove the unknown nonlinear functions, existing works often assume different properties on the latent components (e.g., statistical independence or probability-simplex structures). This work shows that under a carefully designed UML criterion, the existence of a nontrivial null space associated with the underlying mixing system suffices to guarantee identification/removal of the unknown nonlinearity. Compared to prior works, our finding largely relaxes the conditions of attaining PNL identifiability, and thus may benefit applications where no strong structural information on the latent components is known. A finite-sample analysis is offered to characterize the performance of the proposed approach under realistic settings. To implement the proposed learning criterion, a block coordinate descent algorithm is proposed. A series of numerical experiments corroborate our theoretical claims.
On Finite-Sample Identifiability of Contrastive Learning-Based Nonlinear Independent Component Analysis
Jun 14, 2022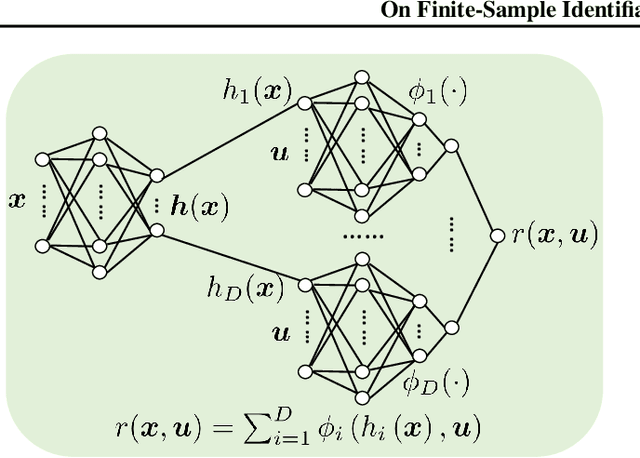

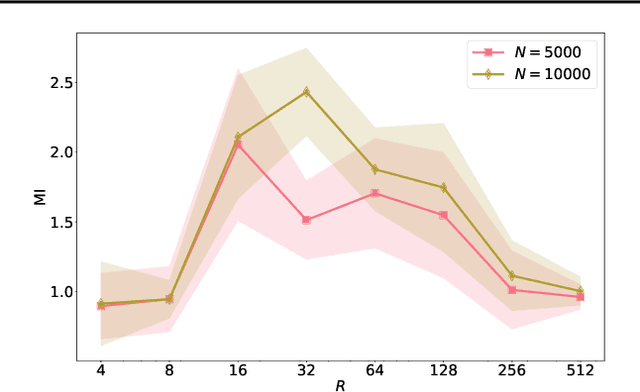
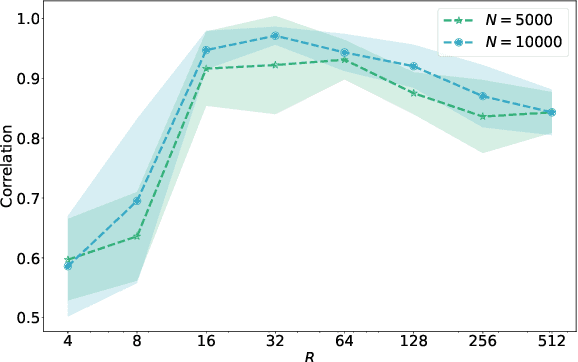
Abstract:Nonlinear independent component analysis (nICA) aims at recovering statistically independent latent components that are mixed by unknown nonlinear functions. Central to nICA is the identifiability of the latent components, which had been elusive until very recently. Specifically, Hyv\"arinen et al. have shown that the nonlinearly mixed latent components are identifiable (up to often inconsequential ambiguities) under a generalized contrastive learning (GCL) formulation, given that the latent components are independent conditioned on a certain auxiliary variable. The GCL-based identifiability of nICA is elegant, and establishes interesting connections between nICA and popular unsupervised/self-supervised learning paradigms in representation learning, causal learning, and factor disentanglement. However, existing identifiability analyses of nICA all build upon an unlimited sample assumption and the use of ideal universal function learners -- which creates a non-negligible gap between theory and practice. Closing the gap is a nontrivial challenge, as there is a lack of established ``textbook'' routine for finite sample analysis of such unsupervised problems. This work puts forth a finite-sample identifiability analysis of GCL-based nICA. Our analytical framework judiciously combines the properties of the GCL loss function, statistical generalization analysis, and numerical differentiation. Our framework also takes the learning function's approximation error into consideration, and reveals an intuitive trade-off between the complexity and expressiveness of the employed function learner. Numerical experiments are used to validate the theorems.
Latent Correlation-Based Multiview Learning and Self-Supervision: A Unifying Perspective
Jun 17, 2021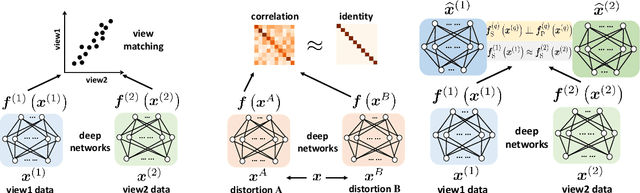
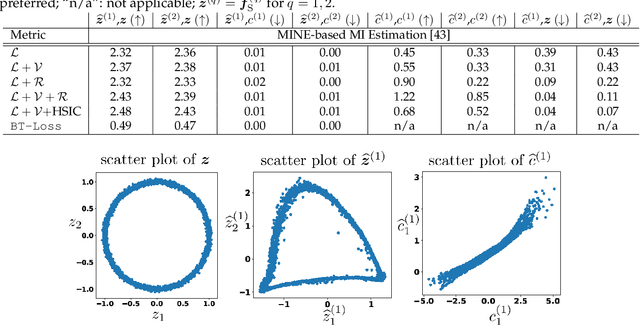
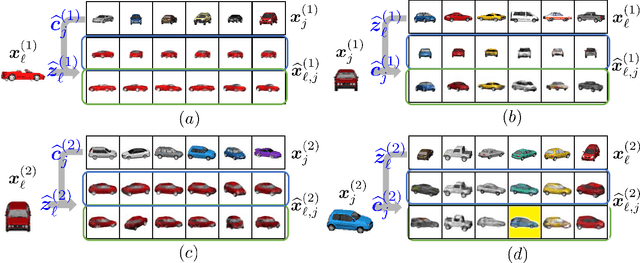
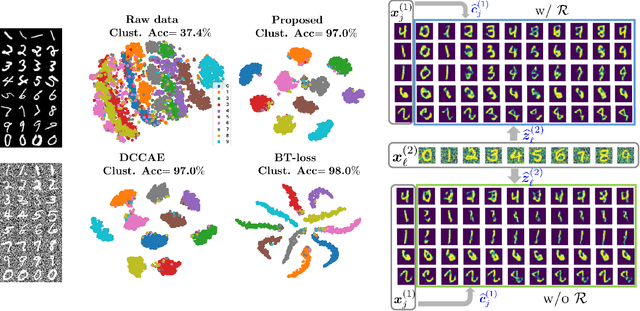
Abstract:Multiple views of data, both naturally acquired (e.g., image and audio) and artificially produced (e.g., via adding different noise to data samples), have proven useful in enhancing representation learning. Natural views are often handled by multiview analysis tools, e.g., (deep) canonical correlation analysis [(D)CCA], while the artificial ones are frequently used in self-supervised learning (SSL) paradigms, e.g., SimCLR and Barlow Twins. Both types of approaches often involve learning neural feature extractors such that the embeddings of data exhibit high cross-view correlations. Although intuitive, the effectiveness of correlation-based neural embedding is only empirically validated. This work puts forth a theory-backed framework for unsupervised multiview learning. Our development starts with proposing a multiview model, where each view is a nonlinear mixture of shared and private components. Consequently, the learning problem boils down to shared/private component identification and disentanglement. Under this model, latent correlation maximization is shown to guarantee the extraction of the shared components across views (up to certain ambiguities). In addition, the private information in each view can be provably disentangled from the shared using proper regularization design. The method is tested on a series of tasks, e.g., downstream clustering, which all show promising performance. Our development also provides a unifying perspective for understanding various DCCA and SSL schemes.
Identifiability-Guaranteed Simplex-Structured Post-Nonlinear Mixture Learning via Autoencoder
Jun 16, 2021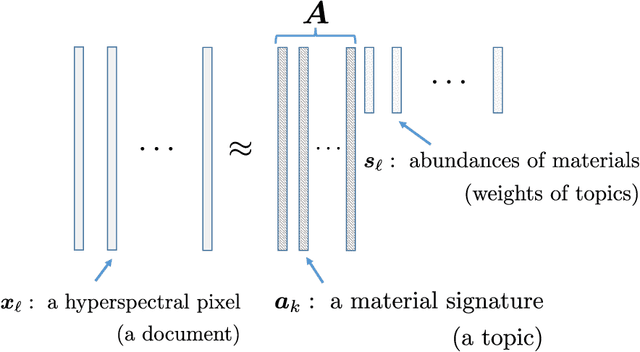
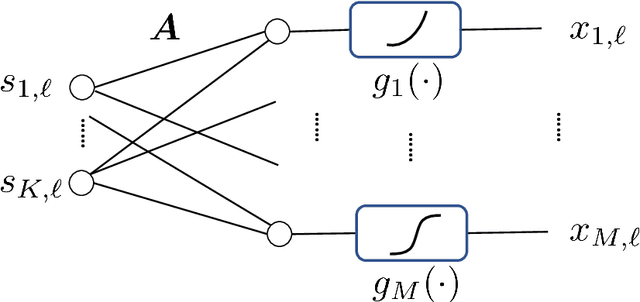

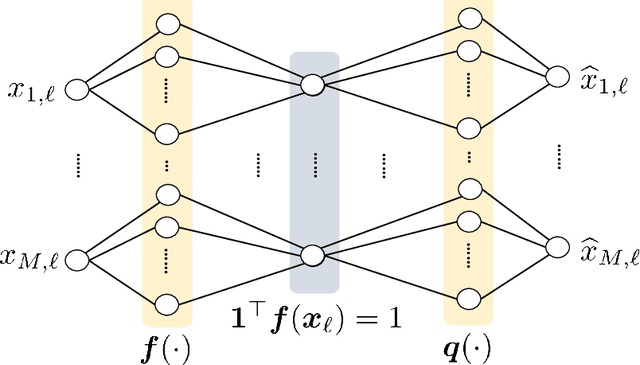
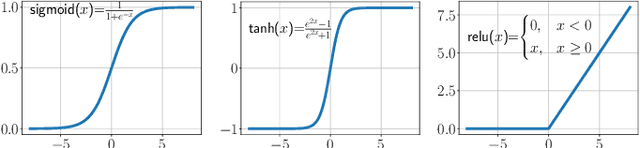
Abstract:This work focuses on the problem of unraveling nonlinearly mixed latent components in an unsupervised manner. The latent components are assumed to reside in the probability simplex, and are transformed by an unknown post-nonlinear mixing system. This problem finds various applications in signal and data analytics, e.g., nonlinear hyperspectral unmixing, image embedding, and nonlinear clustering. Linear mixture learning problems are already ill-posed, as identifiability of the target latent components is hard to establish in general. With unknown nonlinearity involved, the problem is even more challenging. Prior work offered a function equation-based formulation for provable latent component identification. However, the identifiability conditions are somewhat stringent and unrealistic. In addition, the identifiability analysis is based on the infinite sample (i.e., population) case, while the understanding for practical finite sample cases has been elusive. Moreover, the algorithm in the prior work trades model expressiveness with computational convenience, which often hinders the learning performance. Our contribution is threefold. First, new identifiability conditions are derived under largely relaxed assumptions. Second, comprehensive sample complexity results are presented -- which are the first of the kind. Third, a constrained autoencoder-based algorithmic framework is proposed for implementation, which effectively circumvents the challenges in the existing algorithm. Synthetic and real experiments corroborate our theoretical analyses.
Neural Network-Assisted Nonlinear Multiview Component Analysis: Identifiability and Algorithm
Sep 19, 2019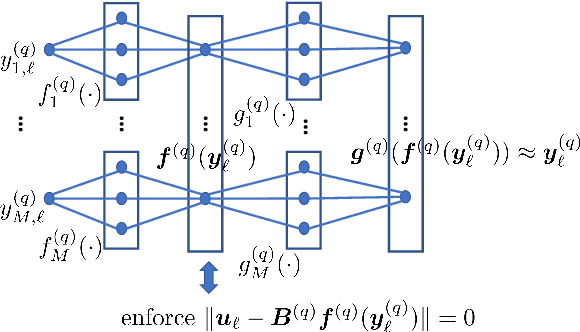
Abstract:Multiview analysis aims at extracting shared latent components from data samples that are acquired in different domains, e.g., image, text, and audio. Classic multiview analysis, e.g., Canonical Correlation Analysis (CCA), tackles this problem via matching the linearly transformed views in a certain latent domain. More recently, powerful nonlinear learning tools such as kernel methods and neural networks are utilized for enhancing the classic CCA. However, unlike linear CCA whose theoretical aspects are clearly understood, nonlinear CCA approaches are largely intuition-driven. In particular, it is unclear under what conditions the shared latent components across the veiws can be identified---while identifiability plays an essential role in many applications. In this work, we revisit nonlinear multiview analysis and address both the theoretical and computational aspects. We take a nonlinear multiview mixture learning viewpoint, which is a natural extension of the classic generative models for linear CCA. From there, we derive a nonlinear multiview analysis criteron. We show that minimizing this criterion leads to identification of the latent shared components up to certain ambiguities, under reasonable conditions. Our derivation and formulation also offer new insights and interpretations to existing deep neural network-based CCA formulations. On the computation side, we propose an effective algorithm with simple and scalable update rules. A series of simulations and real-data experiments corroborate our theoretical analysis.
WristAuthen: A Dynamic Time Wrapping Approach for User Authentication by Hand-Interaction through Wrist-Worn Devices
Oct 22, 2017

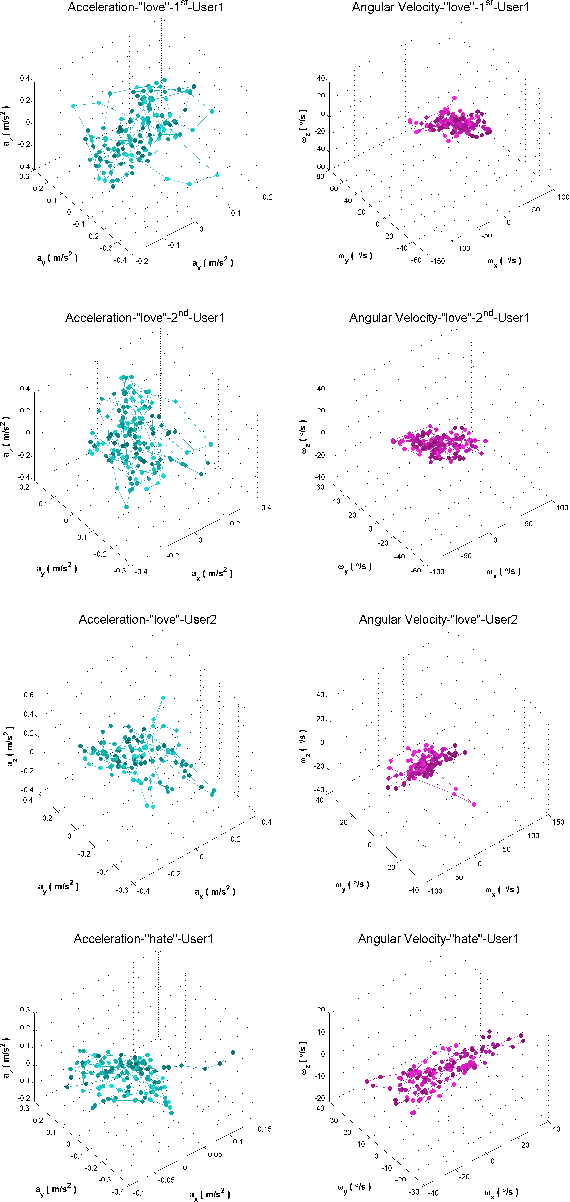
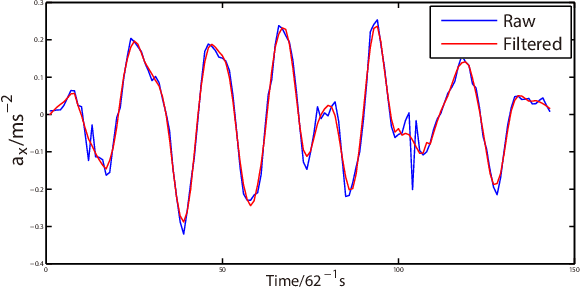
Abstract:The growing trend of using wearable devices for context-aware computing and pervasive sensing systems has raised its potentials for quick and reliable authentication techniques. Since personal writing habitats differ from each other, it is possible to realize user authentication through writing. This is of great significance as sensible information is easily collected by these devices. This paper presents a novel user authentication system through wrist-worn devices by analyzing the interaction behavior with users, which is both accurate and efficient for future usage. The key feature of our approach lies in using much more effective Savitzky-Golay filter and Dynamic Time Wrapping method to obtain fine-grained writing metrics for user authentication. These new metrics are relatively unique from person to person and independent of the computing platform. Analyses are conducted on the wristband-interaction data collected from 50 users with diversity in gender, age, and height. Extensive experimental results show that the proposed approach can identify users in a timely and accurate manner, with a false-negative rate of 1.78\%, false-positive rate of 6.7\%, and Area Under ROC Curve of 0.983 . Additional examination on robustness to various mimic attacks, tolerance to training data, and comparisons to further analyze the applicability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge